I develop my own theory of ko evaluation.
Because of komonster effects, winning (or taking) the ko in my little problem gains 2 points by area scoring, 0.5 point by territory scoring. Neither of these is the "theoretical" value of 4/3 or 1/3. Because the value of plays usually drops over time, kos typically have some komonster effects, although normally not as big as the difference between the dame vs. no dame conditions in area scoring.
Let's look at these effects a little more closely.

Aside from dame, the two plays shown are the last on the board. (Just the top few lines of the board are shown.)
- Click Here To Show Diagram Code
[go]$$B No ko threats, territory scoring
$$ -------------------
$$ | . X O . . . O . . |
$$ | X O O . O O O X X |
$$ | X X O . O X X X . |[/go]
Under Japanese/Korean (territory) scoring, the no ko threat condition makes the player who does not take the gote komonster. So it does not matter which play is made first, regardless of who has sente. As you may verify.

However, in a real game in which the outcome of the ko is uncertain, as a practical matter it is better to take the gote and gain 0.5 point for sure. In this position for Black to fill the ko may gain nothing. She might win it, anyway.

- Click Here To Show Diagram Code
[go]$$B No ko threats, area scoring
$$ -------------------
$$ | . X O . . . O . O |
$$ | X O O . O O O X X |
$$ | X X O . O X X X . |[/go]
Under Chinese/AGA (area) scoring komonster effects could make these plays miai. But we need to consider the dame situation to tell.
If there are no dame, then the two plays are miai.
If there is one dame, then they are miai for Black, because Black gets the dame regardless. For example,
- Click Here To Show Diagram Code
[go]$$B No ko threats, area scoring
$$ -------------------
$$ | 2 X O . . . O 1 O |
$$ | X O O . O O O X X |
$$ | X X O . O X X X . |[/go]

takes dame.

fills ko.
But with one dame they are not miai for White. White should take the gote for a sure 2 point gain plus the dame. If he takes the ko instead:
- Click Here To Show Diagram Code
[go]$$W No ko threats, area scoring
$$ -------------------
$$ | 1 X O . . . O 2 O |
$$ | X O O . O O O X X |
$$ | X X O . O X X X . |[/go]

fills ko.
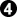
takes dame.
When there are two dame Black should take the gote.
- Click Here To Show Diagram Code
[go]$$B No ko threats, area scoring
$$ -------------------
$$ | 2 X O . . . O 1 O |
$$ | X O O . O O O X X |
$$ | X X O . O X X X . |[/go]

takes dame.

fills ko.
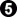
takes dame.
That way she gets both dame, instead of sharing them with White.
And White can take the ko.
- Click Here To Show Diagram Code
[go]$$W No ko threats, area scoring
$$ -------------------
$$ | 1 X O . . . O 2 O |
$$ | X O O . O O O X X |
$$ | X X O . O X X X . |[/go]

fills ko.
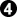
takes dame.

takes dame.
Because either way the dame are shared.
OC, as a practical matter either player should take the gote.

But what does this example say about evaluating plays in the ko? Let us take the value of a play in the gote as given. Either player gains 2 points, for a swing of 4 points. Then we may evaluate the ko ensemble, including any dame. We use swing values to compare different lines of play, as their difference produces swing values.
Code:
If there are no dame, then either winning or taking the ko swings 4 points.
If there is at least one dame, then
1) with an odd number of dame
a) winning the ko swings 4 points,
b) taking the ko swings 2 points;
2) with an even number of dame
a) winning the ko swings 2 points,
b) taking the ko swings 4 points.
If we do not know the number of dame, then the average swing for winning or taking the ko is 3 points, corresponding to the komonster value for territory scoring.

Now, I did not work this out when I started, because I was unaware of area scoring.

But I did work out a general way to evaluate prototypical ko ensembles. I have not run across anything like this way of evaluating kos in the go literature, despite its practical value, as evidenced by my little problem. I started writing a book about it in 1989, but that was before finding out about combinatorial game theory and Professor Berlekamp's work on kos.




