RobertJasiek wrote:
Gérard TAILLE wrote:
See for example my post
https://lifein19x19.com/viewtopic.php?p=280640#p280640 where I used sequences that are not necessarily a perfect play.
In that post, you relied on equality of two counts after two sente sequences. Let me try to construct them for this example:
- Click Here To Show Diagram Code
[go]$$B ordinary sente sequence
$$ ---------------------------
$$ | O . X X . 4 1 3 X 5 X X .
$$ | O O . O X 6 O 2 O X X X .
$$ | . O O O . O O X O X . X .
$$ | . O . O O O . X O X . X .
$$ | . O X X X O X X O X . X .
$$ | . O X X . O O O O X . X .
$$ | O O O O X X X X X X X X .
$$ | . . . . . . . . . . . . .[/go]
- Click Here To Show Diagram Code
[go]$$B alleged alternative sente sequence
$$ ---------------------------
$$ | O . X X . 4 3 1 X 5 X X .
$$ | O O . O X 6 O 2 O X X X .
$$ | . O O O . O O X O X . X .
$$ | . O . O O O . X O X . X .
$$ | . O X X X O X X O X . X .
$$ | . O X X . O O O O X . X .
$$ | O O O O X X X X X X X X .
$$ | . . . . . . . . . . . . .[/go]
For this sequence to make sense, it must be correct for White to reply locally and more specifically at 2.
However, why should this local reply be correct instead of a play elsewhere?
For possibly applying equality of two counts after two sente sequences, White replying locally at 2 must be correct. This must be proved before you can apply equality of two counts after two sente sequences.
Quote:
I called the strategy I used the "Always good exchange strategy".
I do not recall this your phrase. Where did you use it, what is the meaning and what does it tell us?
Quote:
- Click Here To Show Diagram Code
[go]$$B initial position, Black to move
$$ ---------------------------
$$ | O . X X . . b c X . X X .
$$ | O O . O X . O a O X X X .
$$ | . O O O . O O X O X . X .
$$ | . O . O O O . X O X . X .
$$ | . O X X X O X X O X . X .
$$ | . O X X . O O O O X . X .
$$ | O O O O X X X X X X X X .
$$ | . . . . . . . . . . . . .[/go]
Here again I can use this very efficient strategy with success,
Why?
Quote:
showing clearly that black c cannot be a good option in a rich environment.
How do you show it at all and then even very clearly?
Quote:
BTW it is also obvious that black b cannot be either a good option.
(The "either" confuses me.)
Do you presume your rich environment here?
If so, why cannot black b be a good option?
Why is it even obvious?
- Click Here To Show Diagram Code
[go]$$B initial position, Black to move
$$ ---------------------------
$$ | O . X X . . b c X . X X .
$$ | O O . O X . O a O X X X .
$$ | . O O O . O O X O X . X .
$$ | . O . O O O . X O X . X .
$$ | . O X X X O X X O X . X .
$$ | . O X X . O O O O X . X .
$$ | O O O O X X X X X X X X .
$$ | . . . . . . . . . . . . .[/go]
Oops a lot of questions Robert. Before presenting the "Always good exchange strategy" itself I think its interesting to show you how it works in practice on this example.
First of all I put this position P in a rich environment at high temperature T to form a global position G.
Then I look for the most promising local white and black moves.
For white, obviously white "c" is the best move.
For black it is not obvious but black "a" seems the more promising because this move allows to save the four black stones in the center.
Now play a game starting from position G. Each player will play in the environment until the temperature of the environment drops to a temperature t at which white will play at "c" or black will play at "a".
If white plays first at "c" then the score of the game is
S1 = -23.33 + t
If black plays first at "a" then the score of the game is
S2 = -12 - t
(in the calculation of the scores I deleted the term T/2 because it is present in each score and as such it is uninteresting)
Up to this stage nothing is really new. You find that the relevant temperature is when S1 = S2 => t = 5.66 => S1 = S2 = -17.66
Now I begin the "Always good exchange strategy".
For white I do not see another option than the move white "c" we considered => it remains only the black options black "b" and "c" and the question is the following: can black reach a score better than -17.66 by using options "b" or "c"?
Let's begin by black "b".
Now is the first point of the "Always good exchange strategy"
- Click Here To Show Diagram Code
[go]$$B initial position, Black to move
$$ ---------------------------
$$ | O . X X . . 1 . X . X X .
$$ | O O . O X . O 2 O X X X .
$$ | . O O O . O O X O X . X .
$$ | . O . O O O . X O X . X .
$$ | . O X X X O X X O X . X .
$$ | . O X X . O O O O X . X .
$$ | O O O O X X X X X X X X .
$$ | . . . . . . . . . . . . .[/go]
I DECIDE to answer

by

without knowing if it is a good move or not (a tenuki could be better) because it is irrelevant in the "Always good exchange strategy".
From this position we reach the second point of the "Always good exchange strategy"
- Click Here To Show Diagram Code
[go]$$B initial position, Black to move
$$ ---------------------------
$$ | O . X X . 4 1 3 X 5 X X .
$$ | O O . O X 6 O 2 O X X X .
$$ | . O O O . O O X O X . X .
$$ | . O . O O O . X O X . X .
$$ | . O X X X O X X O X . X .
$$ | . O X X . O O O O X . X .
$$ | O O O O X X X X X X X X .
$$ | . . . . . . . . . . . . .[/go]
the following move

may not be the best move (here again a tenuki might be better) but if white answers immediately by

and then
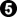

then I claim the sequence


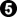

cannot be bad for black. In the startegy I used it is simply "good exchange" for black and it does not mean that the moves chosen are the best one!
Now is the conclusion:
After

the all sequence cannot be bad for black => the score of the game after




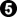

is an upper bound for the score of the game after

followed by the best black and white moves. The score of the game after




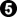

being S3 = -19 I conclude that with

black cannot expect a score better than -19.
Because -19 < -17.66 then option "b" cannot be better than black "a".
If now you consider the option black "c" OBVIOUSLY you can consider the sequence equivalent to the previous one => black cannot expect a score better than -19 and option "c" cannot be better than black "a".



