Hi,
I would like to know if I have correctly understood the method of estimating the value of endgame moves exposed in Robert Jasiek's book Endgame 2.
It is the method that consists in calculating the value per excess move instead of the traditional value.
For example, in a double gote endgame, we use to say that a given endgame is worth 2 points double gote, while another one is one point reverse sente, and since reverse sente is worth twice a double gote, they have the same value.
The new methods consists in counting the total number of excess moves in white's sequence and black's sequence, and dividing the value by this result.
For example in a double gote endgame, there is one white excess move and one black excess move. The sum of these two numbers is called the tally. Here, the tally is two, and we say that the 2 points double gote endgame is actually worth 2/2 = 1 point per move.
The tally of a reverse sente is 1+0 = 1, and a one point reverse sente endgame is thus worth 1/1 = 1 point per move.
The advantage of this method is the evaluation of ko. Let's apply it to this endgame :
Attachment:
Sans titre.png [ 38.7 KiB | Viewed 27057 times ]
The ko in A is simple. If white connects, nothing happens. If black connects nothing happens.
The difference is 1 point (1 prisoner). The tally is 2+1 = 3. The value is 1/3 points per move.
In the ko in B, if black connects, white has no point in E4. But if White connects, it is still unsure if white has a point in E4. It depends if black plays F5. Let's say that there is 1/2 point for white in E4 if white connects the ko.
The difference is 1 prisoner and 1/2 point of territory. The tally is 3. Thus this ko has a value of (1+1/2) / 3 = 1/2 point per move.
In the ko in C if black connects, she has one point in L13, one point in M12. If white K14, white L13, then black answers M12, then white connects. Black has no point, white has one point and two prisoners. The difference is 5, and the tally is 1 + 2 = 3 (the l13-m12 exchange doesn't count).
Thus the value of this ko is 5/3 points per move.
Is it correct ?
In a real game, is this method of evaluation correct ? It seems to me that black has 1 ko threat and white probably 4. Is it possible to read out the optimal sequence ?
In the game, after white C, black connected in L13. What's the value of this move ? Does this possibility change the value of the ko calculated above ?
)
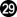(add 300) gains ⅓ point (on average), OC. 
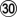and 
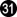each gain 7/9 point, and then 
gains ⅓ point. The 7/9 point figure may be new to some players, so let’s explain that. 
stone, after 
, or vice versa, the result is the same (except for the ko ban). The original position has the same average value as the resulting position, i.e., -⅔.
and 
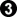each gain ⅓ point, for a local score of 0.
fills ko at 
, 
, and 
(add 200) takes the ko with sente, then switches to the top left corner. 
takes away White’s potential eye, which makes 
and 
a double ko threat. White eliminates that threat and then takes the ko. 
fills the ko
gains nothing because it is a "normal" sente move which can act as a ko threat if temperature in the environment is between 1/3 and 7/9.
in the environment
in the environment
in sente as soon as the temperature of the environment drops to ⅓.