@ robinz:
If you have not done the first problem go back and try it. Although I spent 40 minutes on it and never got close, the resulting discussion helped a lot. Now I still got this one wrong, but in greatly reduced time, and since several Dan players didn't read my mistake, I am not too shaken about it

What the results show is that endgame is probably the most neglected area of study and everyone sucks at it. (As a dan player I would seriously consider Bill's book suggestion. You could probably improve by a stone just by ramping up you yose skillz)


Although I remarked above that everybody sucked at endgame, I guess they suck a different levels (sounds like go ) Endgame skill is based imo 40% on reading and 60% on experience. Higher ranked players should have more of both. My formula for my handicap games is: When we enter yose black should be ahead by rank difference*5 to make it a close game.

Also, do you read while it's your opponents turn? It might not be particularly helpful in the opening, but especially in yose where the possibilities are greatly reduced, even shrubs like us should be capable of reading a few moves in advance.

_________________
While I was teaching the game to a friend of mine, my mother from the other room:
"Cutting? Killing? Poking out eyes? What the hell are you playing?"

You can also calculate the sizes of hundreds of plays.

As for this example, my first impression is that these plays are not independent. My second is that a play here gains about 1 point. My third is that the top is surely Black's best spot, but White may have a play in the bottom.

Closer inspection reveals that a play at the top gains 1.125 points for either player.

Click Here To Show Diagram Code

[go]$$Wc Losing sente
$$ --------------
$$ | . 2 . . . |
$$ | X X O O . |
$$ | . . X O . |
$$ | X X X O O |
$$ | . . 1 O . |
$$ --------------[/go]

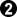
actually gains 1.125 points, too. However, it is a losing sente, as gains 1.5 points in reply, for a loss to White of 0.375 points.

Also, consider this variation at area scoring:

Click Here To Show Diagram Code

[go]$$c Area scoring
$$ --------------
$$ | 3 2 1 4 . |
$$ | X X O O . |
$$ | . . X O . |
$$ | X X X O O |
$$ | . . . O . |
$$ --------------[/go]

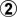
After , sacrifices a stone to take away the eye and set up the ko, leaving this position.

Click Here To Show Diagram Code

[go]$$c Black to play
$$ --------------
$$ | X . X O . |
$$ | X X O O . |
$$ | . . X O . |
$$ | X X X O O |
$$ | . . . O . |
$$ --------------[/go]

Can you tell at a glance where Black should play?

The bottom is a 1 point sente for White (2 points by area scoring), while the top is a 1/3 point ko (1 1/3 points by area scoring).

Click Here To Show Diagram Code

[go]$$Bc Largest play first
$$ --------------
$$ | X 6 X O . |
$$ | X X O O . |
$$ | . . X O . |
$$ | X X X O O |
$$ | . . 5 O . |
$$ --------------[/go]

Black plays the reverse sente and White takes the ko. Black has no ko threat, so the end result is this.

Click Here To Show Diagram Code

[go]$$c Black to play
$$ --------------
$$ | X O O O . |
$$ | X X O O . |
$$ | . . X O . |
$$ | X X X O O |
$$ | . . X O . |
$$ --------------[/go]

White wins by 1 point.

Black should fill the ko.

Click Here To Show Diagram Code

[go]$$Bc Black wins
$$ --------------
$$ | X 5 X O . |
$$ | X X O O . |
$$ | . . X O . |
$$ | X X X O O |
$$ | . 7 6 O . |
$$ --------------[/go]

Black gets the last play to win the game.

Now, isn't that more fun than just saying, the top looks bigger to me?

_________________
The Adkins Principle:
At some point, doesn't thinking have to go on?
— Winona Adkins

Visualize whirled peas.

Everything with love. Stay safe.

This problem can be solved fairly simply, without reading long sequences, by noticing that it is a "corridor" problem, with a long corridor on top and a short corridor on bottom. B should simply play along the longer corridor whenever possible. If W blocks at some point, B switches to the bottom, taking the last point. By starting with a descent, B can avoid worrying about possible ko.

Click Here To Show Diagram Code

[go]$$
$$ --------------
$$ | . 1 . . . |
$$ | X X O O . |
$$ | . . X O . |
$$ | X X X O O |
$$ | . . . O . |
$$ --------------[/go]

The reading in these problems is fun for me because the reading flows around a couple of locations to get a desirable result, compared to eg. L&D or tesuji protracted local sequences, with also an extra emphasis on order of moves. Sure, the specific relevance is + or - one point at the end of the game (which is an important issue occasionally) but it still is reading muscle exercise (insofaras that is a thing ).

_________________
Revisiting Go - Study Journal
My Programming Blog - About the evolution of my go bot.

Click Here To Show Diagram Code

[go]$$W White to play and win.
$$ -----------------------
$$ | . . . . a b . . . . . |
$$ | . . . . c 1 2 . . . . |
$$ | . . O O O X X X X . . |
$$ | . . O . O . . . X . . |
$$ | . . O . O X X . X . . |
$$ | . . O . X X . X . X . |
$$ | . . O . . O O X . . . |
$$ | . . O O O O X X X X X |
$$ | . . O . . X X . X O X |
$$ | . . . O O O X X O . O |
$$ | . . . . . O O X X O . |
$$ ------------------------[/go]

The key decision in this problem is which connection to make, "a", "b", or "c". When I was learning go I realized that they were all the same size, and wondered how to tell which one was best. Sometimes there are tactical reasons for one or the other, such as life and death. But is there a general rule?

It turns out that, when ko is not a consideration, there is. One option is dominant, whatever (non-ko) plays are elsewhere on the board.

_________________
The Adkins Principle:
At some point, doesn't thinking have to go on?
— Winona Adkins

Visualize whirled peas.

Everything with love. Stay safe.