Also, one thing that gives the first player an advantage in a game with alternating play is when the value of plays decrease over time. In general, that is so in go, but sente is the main exception, as sente raises the local temperature.
But early in the game actual sente are rare, so perhaps the Thue-Morse sequence would be good for early play.
First, let's apply it to the first four moves.
- Click Here To Show Diagram Code
[go]$$ Regular go, parallel opening 1
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . 4 . . . . . , . . . . . 1 . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . 2 . . . . . , . . . . . 3 . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
Let both players start on the 4-4 points. White can enforce a parallel opening with  . .
- Click Here To Show Diagram Code
[go]$$ Regular go, parallel opening 2
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . 2 . . . . . , . . . . . 1 . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . 4 . . . . . , . . . . . 3 . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
In this sequence it is Black who can enforce a parallel opening with  . .
- Click Here To Show Diagram Code
[go]$$ Thue-Morse diagonal opening
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . 2 . . . . . , . . . . . 1 . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . 3 . . . . . , . . . . . 2 . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
The Thue-Morse sequence allows White to enforce the diagonal opening. A diagonal opening probably does not favor White, but this fact mitigates any advantage Black might have in the first four moves. So far, so good. 
How about extending the Thue-Morse sequence to the first eight moves?
- Click Here To Show Diagram Code
[go]$$ Thue-Morse 8 move sequence, 1
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . 5 . . 4 . . |
$$ | . . . 2 . . . . . , . . . . . 1 5 6 . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . 3 . . . . . , . . . . . 2 . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
In regular go,  is now considered good in the AI era. However, the two is now considered good in the AI era. However, the two 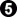 moves make it bad, by transposition turning it into a premature invasion of a 4-4 6-3 corner. This can happen with a parallel opening, as well. moves make it bad, by transposition turning it into a premature invasion of a 4-4 6-3 corner. This can happen with a parallel opening, as well.
- Click Here To Show Diagram Code
[go]$$ Thue-Morse 8 move sequence, 2
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . 2 . . . . . , . . . . . 1 . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . 4 . . |
$$ | . . . . . . . . . . . . . . . 5 5 . . |
$$ | . . . 3 . . . . . , . . . . . 2 . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
 is also OK in regular go, but the two is also OK in regular go, but the two 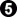 moves give White a broken shape. Neither moves give White a broken shape. Neither 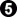 is good in regular go, which is why we don't see it, but the fact that it is sente makes it good in the Thue-Morse sequence. is good in regular go, which is why we don't see it, but the fact that it is sente makes it good in the Thue-Morse sequence.
So it seems to me that maybe the Thue-Morse sequence is not a bad idea for the first four moves. For instance,
- Click Here To Show Diagram Code
[go]$$ Thue-Morse 4 move Go Seigen opening, 1
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . 2 . . . . . , . . . 2 . , 1 . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
In his later years Go Seigen advocated the two space high approach to  , with the idea of the 4-4 follow-up in the top left corner. The Thue-Morse sequence allows White to enforce that position. , with the idea of the 4-4 follow-up in the top left corner. The Thue-Morse sequence allows White to enforce that position.
- Click Here To Show Diagram Code
[go]$$ Thue-Morse 4 move, Go Seigen opening, 2
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . 2 . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . , 1 . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . , . . . . . , . . . . . , . . . |
$$ | . . . 2 . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
Go Seigen also advocated the mukai komoku, which the Thue-Morse sequence allows White to enforce.
All of these possibilities that the B-W-W-B sequence give to White seem to me to reduce Black's first move advantage and also to make for interesting openings.  But later in the game, letting one player make two moves in a row messes up the game. But later in the game, letting one player make two moves in a row messes up the game.
|
 is the only play to win, because White can now prevent Black from making three in a row, and White can win by getting the last move. But if Black makes the second play, any point will allow Black to make three in a row.
is the only play to win, because White can now prevent Black from making three in a row, and White can win by getting the last move. But if Black makes the second play, any point will allow Black to make three in a row.
 omitted )
omitted ) . Whichever one he plays, Black captures all the White stones next.
. Whichever one he plays, Black captures all the White stones next. loses
loses .
. is now considered good in the AI era. However, the two
is now considered good in the AI era. However, the two 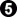 moves make it bad, by transposition turning it into a premature invasion of a 4-4 6-3 corner. This can happen with a parallel opening, as well.
moves make it bad, by transposition turning it into a premature invasion of a 4-4 6-3 corner. This can happen with a parallel opening, as well.