lightvector wrote:
Bill Spight wrote:
As for evaluating kos that remain on the board after the main play or arise in an encore, I am considering a variant of Berlekamp's komaster rule. By that rule if the komaster takes a ko (or plays in a superko) she must immediately resolve the ko or superko. My variant is to allow the opponent to reply instead of having the komaster make more than one move at her turn.
How does one computer-implementably define "komaster"?
I have not gotten that far.

But first, you have to have identified a ko or superko. In Berlekamp's original formulation, the komaster is the player who is permitted to break the ban for that ko but then must continue, at the same turn, to make one or more plays to win the ko. It may not be obvious, but that is a cost to the komaster.
In the case of end of game resolution of kos, "winning" the ko may actually not be desirable. And giving the komaster two or more moves in a row may be a benefit to the komaster. So we give the koloser the option of responding to the komaster. But the komaster still has to resolve the ko.
So for these cases we allow either player to claim the right to be komaster, i.e., to resolve the ko by playing first. The koloser has no right to break the ko ban. If and only if neither player claims the right to be komaster for a ko does that ko remain unresolved.
Since we are talking about hypothetical play, the komaster of a ko is the player who, for that period of play, has the right to resolve that ko.
Quote:
Also, how does one computer-implementably define "resolve"?
A ko is resolved when it no longer exists.
Quote:
It cannot be "fill the ko" because sometimes a player needs to capture a surrounding group rather than filling. And I think "resolving" might also sometimes even involve a non-capture move that leaves the ko mouth to still exist on the board longer. For example, here white should be able to kill everything no matter what, but if black is the first to play and plays "a", then white will need to capture at "b" or "c" to generate a liberty before playing at "d". White must not be forced to fill "b" or "c" thereafter, and neither should we prevent white from being allowed to later capture into "b" or "c" a second time after finishing capturing the black group on the upper side.
- Click Here To Show Diagram Code
[go]$$c
$$ ---------------------------------------
$$ | . X c X O O X . X d O . . . . . . . . |
$$ | X X X O . O X X X O O . . . . . . . . |
$$ | b X O O O O X O O O . . . . . . . . . |
$$ | X O O X X X O O . . . . . . . , . . . |
$$ | O O a X . . . . . . . . . . . . . . . |
$$ | X X X X . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
An interesting position, which I will discuss below.

Quote:
It seems to me also if the opponent's "reply" is an arbitrary move elsewhere on the board that is threatening in some way, and the opponent keeps playing such moves, one must allow a potentially arbitrary number of responses by the komaster to those moves before "resolving" the ko - is there a way to handle this?
The komaster does not have to answer any arbitrary play. Her job is to resolve the ko. As long as she can do so safely, all hypothetical plays by the koloser are ignored. Details may need to be worked out.

- Click Here To Show Diagram Code
[go]$$c Ambiguous temperature
$$ ---------------------------------------
$$ | . X c X O O X . X d O . . . . . . . . |
$$ | X X X O . O X X X O O . . . . . . . . |
$$ | b X O O O O X O O O . . . . . . . . . |
$$ | X O O X X X O O . . . . . . . , . . . |
$$ | O O a X . . . . . . . . . . . . . . . |
$$ | X X X X . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
While this is a scorable corner, it has an ambiguous temperature.
- Click Here To Show Diagram Code
[go]$$Bc Black first
$$ ---------------------------------------
$$ | . X . X O O X . X . O . . . . . . . . |
$$ | X X X O . O X X X O O . . . . . . . . |
$$ | 2 X O O O O X O O O . . . . . . . . . |
$$ | X O O X X X O O . . . . . . . , . . . |
$$ | O O 1 X . . . . . . . . . . . . . . . |
$$ | X X X X . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]

raises the temperature quite high, as it threatens to recolor many White intersections.

- Click Here To Show Diagram Code
[go]$$Wc White first
$$ ---------------------------------------
$$ | . X . X O O X . X . O . . . . . . . . |
$$ | X X X O . O X X X O O . . . . . . . . |
$$ | 1 X O O O O X O O O . . . . . . . . . |
$$ | X O O X X X O O . . . . . . . , . . . |
$$ | O O 2 X . . . . . . . . . . . . . . . |
$$ | X X X X . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
After

the local temperature is 0, as either player can play at
2. What these two sequences show is that we can regard the local temperature as lying between 0 and -1, inclusive. At or below temperature zero, either player can make a play, but neither player has to make a play.
For scoring purposes what we want is a position unambiguously with temperature -1. Such as the following position.
- Click Here To Show Diagram Code
[go]$$Wc Temperature -1
$$ ---------------------------------------
$$ | . X . X O O X . X . O . . . . . . . . |
$$ | X X X O . O X X X O O . . . . . . . . |
$$ | O X O O O O X O O O . . . . . . . . . |
$$ | . O O X X X O O . . . . . . . , . . . |
$$ | O O X X . . . . . . . . . . . . . . . |
$$ | X X X X . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
Assuming that White wishes to show that Black is dead, we presumably will reach this position via the White first diagram above.

By human rules White may have to reopen play in order to do so.
Now, in this position neither player will claim to be komaster for either of the double kos.
- Click Here To Show Diagram Code
[go]$$Wc White claims to be komaster for ko 
$$ ---------------------------------------
$$ | . X 1 B O O X . X . O . . . . . . . . |
$$ | X X X O 4 O X X X O O . . . . . . . . |
$$ | O X O O O O X O O O . . . . . . . . . |
$$ | 2 O O X X X O O . . . . . . . , . . . |
$$ | O O X X . . . . . . . . . . . . . . . |
$$ | X X X X . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]

at

After
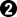
White is forced to resolve the ko by filling at

, losing a large group. OC, it does no good for Black to claim komaster status, either.
So in the encore White will recolor the Black points on the right before tackling the very corner.

In fact, White could start off that way, as in the following diagram.
- Click Here To Show Diagram Code
[go]$$Wc Variation
$$ ---------------------------------------
$$ | . X . X O O X 3 X 1 O . . . . . . . . |
$$ | X X X O . O X X X O O . . . . . . . . |
$$ | . X O O O O X O O O . . . . . . . . . |
$$ | B O O X X X O O . . . . . . . , . . . |
$$ | O O 2 X . . . . . . . . . . . . . . . |
$$ | X X X X . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]
Now let White claim komaster status for the

ko. Black could do so, as well, and fill the ko safely — for the moment, anyway. But why bother?

- Click Here To Show Diagram Code
[go]$$Wcm5 Variation, continued
$$ ---------------------------------------
$$ | 7 X 5 X O O . O . O O . . . . . . . . |
$$ | X X X O . O . . . O O . . . . . . . . |
$$ | 1 X O O O O . O O O . . . . . . . . . |
$$ | B O O X X X O O . . . . . . . , . . . |
$$ | O O X X . . . . . . . . . . . . . . . |
$$ | X X X X . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]

at

As komaster White takes the ko and, without objection, resolves it by filling it. Then White claims komaster status for the remaining corner ko and takes and resolves it. OC, Black could claim komaster status for the last ko, as well, but to no avail. She would just have to fill it and let White capture.




