Gérard TAILLE wrote:
Yes Bill, we have to make our maximum to keep things as simple as possible.
When I analyse a position in order to discover the best moves, the miai value and the mast value, the first phase consists of finding the best sequences. Here my view is that we must make our maximum to play the technically best moves. We must avoid technically bad moves as for example a bad order of the moves. In order to reach this goal I prefer to use a rich environment ε, 2ε, 3ε, 4ε ...
That way I can see a difference between the sequences
g1 + g2 + g3 - g4 + g5 - g6 ... and g1 - g2 + g3 + g4 + g5 - g6 ... = 2(g2 -g4) = 4ε
As soon as the best sequence has been discovered then I prefer to use the usual ideal environment to give a result as simple as possible.
OC if I want to show a small particularity of the position, depending of the environment, then I can build a complete environment.
What is your own approach Bill?
My main concern these days is spreading and promoting thermography in go. Thermography was invented by Conway in the 1970s and published in
On Numbers and Games. A friend lent me a copy and thought that thermography might be of interest in go. Then thermography was defined in terms of applying a tax to plays. It seemed to produce the same evaluations of go positions and plays as methods that go players already used — I was unaware of the problems with complex ko positions at that time —, so I did not see any benefit from it.
That changed for me when I attended a lecture by Berlekamp in 1994 or 5 in which he presented his komaster theory. Despite the fact that it left open the question of whether the conditions for komaster were met in actual play, it provided a considerably more tractable theory for evaluating complex ko positions than the ko theory I had developed. My theory included all of the environment in the ko ensemble. The problem with doing that is that to evaluate a ko you have to read out the whole board. But, OC, if you can do that you don't need any theory.

I joined a small group consisting of Berlekamp, some of his students and former students, and visiting scholars, and myself, which mainly studied komaster theory. At first I solved problems by opining correct play and then drawing the thermograph from that. This irked Berlekamp, who was around 3 kyu, because he contended that thermography provided a way of finding correct play. He was right, OC. Thermographic lines generated by incorrect play do not appear in the final thermograph.

At temperature 0, where the game is played out, thermography indicates correct play, but that is guaranteed only by exhaustive search, or by perhaps other means of proving correct play. (If there is an encore, thermography may apply below temperature 0, but in go this is highly dependent upon the rules.) What thermography does is to provide correct play
at each temperature. A play or line of play may be incorrect at one temperature and correct at another. Any play, given otherwise correct play, that produces the best result at a given temperature for the player, will indicate a point on the thermograph at that temperature.
So, for instance,
- Click Here To Show Diagram Code
[go]$$W White to play
$$ ---------------------
$$ | X 1 X O X X O O . |
$$ | 3 X O O X X O O O |
$$ | X 5 O X X X O O O |
$$ | 4 O O X . X O O O |
$$ | X O X X . X O O O |
$$ | 2 X . . . X O O . |
$$ | . X . . . X X O O |
$$ | X X . . . . X X X |
$$ | . . . . . . . . . |
$$ ---------------------[/go]
This line of play gives the best result for Black at or below temperature 1 and will thus indicate the wall of the thermograph in that temperature range.

- Click Here To Show Diagram Code
[go]$$W White to play
$$ ---------------------
$$ | X 1 X O X X O O . |
$$ | 3 X O O X X O O O |
$$ | X 5 O X X X O O O |
$$ | . O O X . X O O O |
$$ | X O X X . X O O O |
$$ | . X . . . X O O . |
$$ | . X . . . X X O O |
$$ | X X . . . . X X X |
$$ | . . . . . . . . . |
$$ ---------------------[/go]
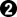
,
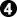
elsewhere (in the environment)
This result is 2 points worse for Black on the board than the previous result, so it is preferable when t > 1.
Also,
- Click Here To Show Diagram Code
[go]$$W White to play
$$ ---------------------
$$ | 1 X O X . . . . . |
$$ | X O O X . . . . . |
$$ | 3 O X X . . . . . |
$$ | 2 O X . . . . . . |
$$ | X X X . . . . . . |
$$ | . . . . . . . . . |
$$ | . . . . . . . . . |
$$ | . . . . . . . . . |
$$ | . . . . . . . . . |
$$ ---------------------[/go]
This is the best Black can do at temperature 0, and indicates the wall of the thermograph at that temperature.
- Click Here To Show Diagram Code
[go]$$W White to play
$$ ---------------------
$$ | 1 X O X . . . . . |
$$ | X O O X . . . . . |
$$ | 3 O X X . . . . . |
$$ | C O X . . . . . . |
$$ | X X X . . . . . . |
$$ | . . . . . . . . . |
$$ | . . . . . . . . . |
$$ | . . . . . . . . . |
$$ | . . . . . . . . . |
$$ ---------------------[/go]
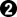
elsewhere
OC, above temperature 0 Black will not play
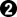
.

At temperature 0 one player or other will fill the dame. Doing so did not change the score, OC, before the Japanese 1989 rules, which scores the White group as 0 if the dame,

, is unfilled. In fact, the Japanese used to be quite proud of not filling the dame. (The J89 rules included a loophole which allowed players to continue their practice of leaving dame unfilled before scoring. But that has led to problems since then.)



