Hi,
I would like to know if I have correctly understood the method of estimating the value of endgame moves exposed in Robert Jasiek's book Endgame 2.
It is the method that consists in calculating the value per excess move instead of the traditional value.

For example, in a double gote endgame, we use to say that a given endgame is worth 2 points double gote, while another one is one point reverse sente, and since reverse sente is worth twice a double gote, they have the same value.

The new methods consists in counting the total number of excess moves in white's sequence and black's sequence, and dividing the value by this result.
For example in a double gote endgame, there is one white excess move and one black excess move. The sum of these two numbers is called the tally. Here, the tally is two, and we say that the 2 points double gote endgame is actually worth 2/2 = 1 point per move.
The tally of a reverse sente is 1+0 = 1, and a one point reverse sente endgame is thus worth 1/1 = 1 point per move.

The advantage of this method is the evaluation of ko. Let's apply it to this endgame :



The ko in A is simple. If white connects, nothing happens. If black connects nothing happens.
The difference is 1 point (1 prisoner). The tally is 2+1 = 3. The value is 1/3 points per move.

In the ko in B, if black connects, white has no point in E4. But if White connects, it is still unsure if white has a point in E4. It depends if black plays F5. Let's say that there is 1/2 point for white in E4 if white connects the ko.
The difference is 1 prisoner and 1/2 point of territory. The tally is 3. Thus this ko has a value of (1+1/2) / 3 = 1/2 point per move.

In the ko in C if black connects, she has one point in L13, one point in M12. If white K14, white L13, then black answers M12, then white connects. Black has no point, white has one point and two prisoners. The difference is 5, and the tally is 1 + 2 = 3 (the l13-m12 exchange doesn't count).
Thus the value of this ko is 5/3 points per move.

Is it correct ?

In a real game, is this method of evaluation correct ? It seems to me that black has 1 ko threat and white probably 4. Is it possible to read out the optimal sequence ?

In the game, after white C, black connected in L13. What's the value of this move ? Does this possibility change the value of the ko calculated above ?

This method is not new. It goes back to some time in the 20th century. John Fairbairn can tell us when, I think.



It is a good idea to start, not with the calculation of moves, but with the calculation of the local territorial count. By convention we do so from Black's point of view.

If Black connects at a the local score is 0. If White takes and wins the ko the local score is -1. From this we may calculate the local count to be -⅓. Then when Black plays from a position worth, on average, -⅓ to one worth 0, she gains ⅓ point on average. Similarly, when White play from a position worth -⅓ to one worth -1 in 2 moves, he gains ⅓ point per move, on average.



At this point, each player has possible local plays at D-05 and F-05. Let's look at F-05, the non-ko play, first. If Black plays at F-05 the local count is ⅓ in a simple ko, and each play in the ko gains ⅓. (I'll leave out the "on average" now, as we all understand that.) If White plays at F-05 and then connects the simple ko the local score is -1. But if Black in reply takes and wins the ko the local score is +1. So after White F-05 the local count is -⅓ and each play in the ko gains ⅔. Now let's look at D-05. If White connects at D-05 the local count is fairly obviously -½ and each play gains ½. If Black takes the ko at D-05 and then connects it the local score is +1. On average it is the case that each player does best to play in the ko, that the local count is 0, and that each play gains ½ point. However, best play depends on the ko threat situation. If White can win the ko, for instance, instead of connecting the ko White should usually play at F-05.

(Edit: Next paragraph corrected for silly goof. )

Now let's look at C. If Black wins the ko the local score is +2. If White takes the ko and Black fills the second ko, the local count is +⅓ and each play now gains ⅓. If White takes the second ko it is plainly sente, and after Black replies we have what we may recognize as a 1 point ko. If White now connects the ko the local score is -3, so the current count is -2. As this is the result of sente, the count after White takes the first ko is also -2. In that case Black filling the second ko gains 2⅓ and so White takes the first ko with sente. That means that the original count is ⅓ and Black filling the original ko gains 1⅔. In common parlance we say that this is a 1⅔ point sente, but really, it is the reverse sente that gains 1⅔.



The calculation of counts and average gains is correct, but, as indicated, after White takes the ko in the center with sente, if White can win the bottom left ko, White's best play may be at F-05. It may be worth reading that out.

_________________
The Adkins Principle:
At some point, doesn't thinking have to go on?
— Winona Adkins

Visualize whirled peas.

Everything with love. Stay safe.

Wow ! Thank you for this detailed answer.
I will study it carefully.

Oops! I miscounted. I shall correct the calculation immediately.

_________________
The Adkins Principle:
At some point, doesn't thinking have to go on?
— Winona Adkins

Visualize whirled peas.

Everything with love. Stay safe.

Let me just add what Bill has not mentioned yet.



This is a lazy, dangerous calculation, which sometimes fails when a white follower has a positive count. The safe calculation writes all counts from Black's value perspective, that is, counts favouring White are written as negative numbers. Therefore:

The count is -1/2 in E4 if white connects the ko. This ko has the move value (1 - (-1/2)) / 3 = (1 + 1/2) / 3 = 1/2.

***

After Black M12, see the book for an ordinary 2-stage ko, whose evaluation Bill presumes.

Thanks for the complements.

This one is actually off. The calculation in itself may be correct, but it does not account for the fact that it may be better for black to connect at l13 in response to white k14.

To get a fair abstract situation estimate, you can either count the average of the results of white or black playing first (with any sente follow-up moves included), or you can add a stone to both players and count that result. Whichever is higher for the defender is the ’correct’ value.

If black connects the ko, you define the result as b+2. If instead white plays k14 and gets to play l13, forcing black m12, the expected score in that situation (without white playing k13) is w+2. (You may need to read further on two-step kos to understand why.) Therefore, this calculation suggests that the expected score in the viewed area is +-0.

If white plays k14 and black answers with l13, however, the result is otherwise w+1 (captured stone) plus b+1 (point at m12) for a net score of 0, but a ko shape remains hanging which is ⅓ points favourable for black. Therefore the result is b+⅓. Because this is higher than the above avg(w first, b first), which we found to be +-0, this is generally the ’correct result’.

If it helps any, this one has several ko fights right at the end of the game. It's Fujisawa 4p's victory at the Hiroshima Al Cup.

Take care.

_________________
一碁一会

The last ko fight of the Fujisawa Rina (W) - Son Makoto game.

Click Here To Show Diagram Code

[go]$$Bcm29 Finale, W332 fills ko
$$ ---------------------------------------
$$ | 2 X 3 X . X . X O O O O . . . O O O X |
$$ | B O X X X . X X O O X O O O O O O X 1 |
$$ | O O O X O X X X X X X O X O X O X X X |
$$ | O O O O O O X O O X . O X X X O X X . |
$$ | X O X X O O O O . X O O O O X X X . . |
$$ | X X X O O X O O X X . . X X X X O X . |
$$ | . . . X . X X O O . O O O X O X O X . |
$$ | X X X X X X . X O O O X O O O O O X . |
$$ | O O O O O X . X X O X X X . O O X X . |
$$ | O X X X X X . . . X X O X X X O O X X |
$$ | O O O X X X X X X X . O O O O . . O X |
$$ | O . . O O X O O O X O . . . . . . O X |
$$ | O . O . O X O . O X O O O . . . O . O |
$$ | . O . O . O O O O X O X O . . O O O . |
$$ | . . O . O O X X X O X X O O O O X O O |
$$ | O . . O O O O X . O X X O X O X X X O |
$$ | . O O O X O O X O X X O O X X X . X O |
$$ | O X O X X X X X O X . X O X . . X . X |
$$ | . X X . X . . . X . X X X . . . . X . |
$$ ---------------------------------------[/go]

(add 300) gains ⅓ point (on average), OC. and each gain ⁷/₉ point, and then gains ⅓ point. The ⁷/₉ point figure may be new to some players, so let’s explain that.

Counting the captured stone, after the local count in the top left corner is -⅔, and after , which gains ⅓ point, the local score is -1. But suppose that instead White takes the ko at 31 and fills it. Then the local score will be -3. That means that 3 plays gain a total of 2⅓ points, for a average gain of ⁷/₉ point. There are two kos in this corner, one where each play gains ⅓ point, and one where each play gains ⁷/₉ point.

So what is the local count of this corner position?

Click Here To Show Diagram Code

[go]$$Bc Miai
$$ ----------------
$$ | . X . X . X . X
$$ | X O X X X . X X
$$ | O O O X O X X X
$$ | O O O O O O X O
$$ | X O X X O O O O
$$ | X X X O O X O O
$$ | . . . X . X X O
$$ | X X X X X X . X[/go]

Black has only one best move, and White has only one move, which do not interfere with each other. We may regard them as miai.

Click Here To Show Diagram Code

[go]$$Bc Miai
$$ ----------------
$$ | W X B X . X . X
$$ | X O X X X . X X
$$ | O O O X O X X X
$$ | O O O O O O X O
$$ | X O X X O O O O
$$ | X X X O O X O O
$$ | . . . X . X X O
$$ | X X X X X X . X[/go]

Whether Black plays and then White plays , or vice versa, the result is the same (except for the ko ban). The original position has the same average value as the resulting position, i.e., -⅔.

Click Here To Show Diagram Code

[go]$$Bc Black wins ko
$$ ----------------
$$ | 3 X 1 X . X . X
$$ | X O X X X . X X
$$ | O O O X O X X X
$$ | O O O O O O X O
$$ | X O X X O O O O
$$ | X X X O O X O O
$$ | . . . X . X X O
$$ | X X X X X X . X[/go]

and each gain ⅓ point, for a local score of 0.

Click Here To Show Diagram Code

[go]$$Wc White wins ko
$$ ----------------
$$ | 1 B 3 X . X . X
$$ | X O X X X . X X
$$ | O O O X O X X X
$$ | O O O O O O X O
$$ | X O X X O O O O
$$ | X X X O O X O O
$$ | . . . X . X X O
$$ | X X X X X X . X[/go]

fills ko at
, , and each gain ⁷/₉ point, for a local score of -3.

This is one of those (almost) never see sequences in go, because if Black cannot win both kos she can answer at 3. Since White’s moves gain more than Black’s, it is very likely that White can take the ko with sente, and then win the ⅓ point ko. For Black to win the ko she must have larger ko threats than White needs to have. Also, if Black plays first, the move gains ⅓ point, but does not generate a ko ban, so Black also needs one more ko threat than White in that case, although they do not need to be so large.

Now let’s back the original position up one move by White. How much is this position worth, on average?

Click Here To Show Diagram Code

[go]$$Bc Miai
$$ ----------------
$$ | . X . X . X . X
$$ | X O X X X . X X
$$ | . O O X O X X X
$$ | O O O O O O X O
$$ | X O X X O O O O
$$ | X X X O O X O O
$$ | . . . X . X X O
$$ | X X X X X X . X[/go]

This corner position is worth -⅓ point.

Click Here To Show Diagram Code

[go]$$Bc Miai
$$ ----------------
$$ | . X B X . X . X
$$ | X O X X X . X X
$$ | W O O X O X X X
$$ | O O O O O O X O
$$ | X O X X O O O O
$$ | X X X O O X O O
$$ | . . . X . X X O
$$ | X X X X X X . X[/go]

We can see this by playing the miai.

Let’s back up the position one more move, by Black. How much is this corner position worth?

Click Here To Show Diagram Code

[go]$$Bc Earlier position
$$ ----------------
$$ | . X . X . X . X
$$ | . O X X X . X X
$$ | . O O X O X X X
$$ | O O O O O O X O
$$ | X O X X O O O O
$$ | X X X O O X O O
$$ | . . . X . X X O
$$ | X X X X X X . X[/go]

Well, let’s look at the result if White plays first.

Click Here To Show Diagram Code

[go]$$Wc White first
$$ ----------------
$$ | . X . X . X . X
$$ | 1 O X X X . X X
$$ | . O O X O X X X
$$ | O O O O O O X O
$$ | X O X X O O O O
$$ | X X X O O X O O
$$ | . . . X . X X O
$$ | X X X X X X . X[/go]

This position is worth -1, so the previous position is worth -⅔, and each play gains ⅓ point.

Click Here To Show Diagram Code

[go]$$Bc Possible
$$ ----------------
$$ | 4 X 3 X . X . X
$$ | 1 O X X X . X X
$$ | 2 O O X O X X X
$$ | O O O O O O X O
$$ | X O X X O O O O
$$ | X X X O O X O O
$$ | . . . X . X X O
$$ | X X X X X X . X[/go]

OC, this is one possible sequence of play, with each play gaining ⅓ point.

——

Back to the game.

Click Here To Show Diagram Code

[go]$$Bcm29 Finale, W332 fills ko
$$ ---------------------------------------
$$ | 2 X 3 X . X . X O O O O . . . O O O X |
$$ | B O X X X . X X O O X O O O O O O X 1 |
$$ | O O O X O X X X X X X O X O X O X X X |
$$ | O O O O O O X O O X . O X X X O X X . |
$$ | X O X X O O O O . X O O O O X X X . . |
$$ | X X X O O X O O X X . . X X X X O X . |
$$ | . . . X . X X O O . O O O X O X O X . |
$$ | X X X X X X . X O O O X O O O O O X . |
$$ | O O O O O X . X X O X X X . O O X X . |
$$ | O X X X X X . . . X X O X X X O O X X |
$$ | O O O X X X X X X X . O O O O . . O X |
$$ | O . . O O X O O O X O . . . . . . O X |
$$ | O . O . O X O . O X O O O . . . O . O |
$$ | . O . O . O O O O X O X O . . O O O . |
$$ | . . O . O O X X X O X X O O O O X O O |
$$ | O . . O O O O X . O X X O X O X X X O |
$$ | . O O O X O O X O X X O O X X X . X O |
$$ | O X O X X X X X O X . X O X . . X . X |
$$ | . X X . X . . . X . X X X . . . . X . |
$$ ---------------------------------------[/go]

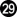
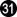
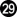
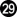
at would also gain ⅓ point, but is technically correct, because White would then take either ko, resulting in a miai. Each player could then win one ko. gives Black the possibility of winning both kos. On this board he does not have the ko threats to do that, but he made the technically correct play.

Earlier:

Click Here To Show Diagram Code

[go]$$Bcm95 W300 takes the ko
$$ ---------------------------------------
$$ | . X . X . X . X O O O O . . . O 2 O 1 |
$$ | 3 O X X X . X X O O X O O O O O O X W |
$$ | . O O X O X X X X X X O X O X O X X X |
$$ | O O O O O O X O . , . O X X X O X X . |
$$ | X O X X O O O O . X O O O O X X X . . |
$$ | X X X O O X O O X X . . X X 5 X O X . |
$$ | . . . X . X X O O . O O O X O X O X . |
$$ | X X X X . X . X O O O X O O 4 O O X . |
$$ | O O O O O X . X X O X X X . O O X X . |
$$ | O X X X . X . . . X X O X X X O O X X |
$$ | O O O X X X X X X X . O O O O . . O X |
$$ | . X X O O X O O O X O . . . . . . O X |
$$ | . X O . O X O . O X O O O . . . . . O |
$$ | . O . O . O O O O X O X O . . O O O . |
$$ | . . . . O O X X X O X X O O O O X O O |
$$ | . . . O O O O X . O X X O X O X X X O |
$$ | . O O O X O O X O X X O O X X X . X O |
$$ | O X O X X X X X . X O X O X . . X . X |
$$ | . X X . X . . . . . . X X . . . . . . |
$$ ---------------------------------------[/go]

(add 200) takes the ko with sente, then switches to the top left corner. takes away White’s potential eye, which makes and a double ko threat. White eliminates that threat and then takes the ko.

Click Here To Show Diagram Code

[go]$$Wcm100 Sente ko
$$ ---------------------------------------
$$ | 3 X . X . X . X O O O O . . . O O O X |
$$ | X O X X X . X X O O X O O O O O O X 2 |
$$ | 1 O O X O X X X X X X O X O X O X X X |
$$ | O O O O O O X O . , . O X X X O X X . |
$$ | X O X X O O O O . X O O O O X X X . . |
$$ | X X X O O X O O X X . . X X X X O X . |
$$ | . . . X . X X O O . O O O X O X O X . |
$$ | X X X X . X . X O O O X O O O O O X . |
$$ | O O O O O X . X X O X X X . O O X X . |
$$ | O X X X . X . . . X X O X X X O O X X |
$$ | O O O X X X X X X X . O O O O . . O X |
$$ | . X X O O X O O O X O . . . . . . O X |
$$ | . X O . O X O . O X O O O . . . . . O |
$$ | . O . O . O O O O X O X O . . O O O . |
$$ | . . . . O O X X X O X X O O O O X O O |
$$ | . . . O O O O X . O X X O X O X X X O |
$$ | . O O O X O O X O X X O O X X X . X O |
$$ | O X O X X X X X . X O X O X . . X . X |
$$ | . X X . X . . . . . . X X . . . . . . |
$$ ---------------------------------------[/go]

It does not matter on this board, but W300 would have been technically better in the top left corner. To have any hope of winning both kos Black must fill the ko in the top right, but then White gets to play the favorable sente ko in the top left. Black needs larger ko threats than White does.

_________________
The Adkins Principle:
At some point, doesn't thinking have to go on?
— Winona Adkins

Visualize whirled peas.

Everything with love. Stay safe.

Someone had fun...

Take care

_________________
一碁一会

I do not understand how the value of in the first diagram (⅓ point) can be different than the value of in the second diagram (⁷/₉ point).
I am not sure of my calculation but I found the values:
in diagram 1 : ⁵/₉ point
in diagram 1 : ⅓ point
in diagram 2 : ⁵/₉ point
and in diagram 2 : ⁷/₉ point
and the score of the original position : -⁸/₉ point

IOW I agree with you Bill concerning the value of , and but I do not understand how you found the values of and and why these values can be different.

is gote-like. raises the local temperature to ⁷/₉ and is like sente.

Click Here To Show Diagram Code

[go]$$Bc Count = -⅔
$$ ----------------
$$ | W X B X . X . X
$$ | . O X X X . X X
$$ | O O O X O X X X
$$ | O O O O O O X O
$$ | X O X X O O O O
$$ | X X X O O X O O
$$ | . . . X . X X O
$$ | X X X X X X . X[/go]

1 prisoner

Draw the thermograph of this ko (with no ko threats). Its mast rises vertically from temperature ⅓ at count -⅔.

Click Here To Show Diagram Code

[go]$$Bc Count = -⅔
$$ ----------------
$$ | . X . X . X . X
$$ | X O X X X . X X
$$ | O O O X O X X X
$$ | O O O O O O X O
$$ | X O X X O O O O
$$ | X X X O O X O O
$$ | . . . X . X X O
$$ | X X X X X X . X[/go]

The thermograph of this position will be the same, except that its mast is colored red up to temperature ⁷/₉.

Edit: Assuming no ko threats, the left wall of the second thermograph will be the same as the right wall below temperature ⅓, on the line v = -1 + t.

That's because minimax play will go this way.

Click Here To Show Diagram Code

[go]$$Wc White first
$$ ----------------
$$ | 1 X 2 X . X . X
$$ | B O X X X . X X
$$ | O O O X O X X X
$$ | O O O O O O X O
$$ | X O X X O O O O
$$ | X X X O O X O O
$$ | . . . X . X X O
$$ | X X X X X X . X[/go]

fills the ko.

Click Here To Show Diagram Code

[go]$$Bc Black first
$$ ----------------
$$ | 2 X 1 X . X . X
$$ | B O X X X . X X
$$ | O O O X O X X X
$$ | O O O O O O X O
$$ | X O X X O O O O
$$ | X X X O O X O O
$$ | . . . X . X X O
$$ | X X X X X X . X[/go]

elsewhere, fills the ko

_________________
The Adkins Principle:
At some point, doesn't thinking have to go on?
— Winona Adkins

Visualize whirled peas.

Everything with love. Stay safe.

Three such positions add to -2.

_________________
The Adkins Principle:
At some point, doesn't thinking have to go on?
— Winona Adkins

Visualize whirled peas.

Everything with love. Stay safe.

Click Here To Show Diagram Code

[go]$$B
$$ -----------------
$$ | . X . X . . . |
$$ | X O X X . . . |
$$ | O O O X . . . |
$$ | . . . . . . . |
$$ | . . . . . . . |
$$ | . . . . . . . |
$$ | . . . . . . . |
$$ -----------------[/go]

I agree with your analysis Bill but I do not not understand your conclusion (I mean: gains ⁷/₉ point)

Click Here To Show Diagram Code

[go]$$W
$$ -----------------
$$ | a X b X . . . |
$$ | X O X X . . . |
$$ | O O O X . . . |
$$ | . . . . . . . |
$$ | . . . . . . . |
$$ | . . . . . . . |
$$ | . . . . . . . |
$$ -----------------[/go]

After the white "a" black "b" exchange the score of the resulting position is -⅔ and the miai value is ⅓.
What happens if the temperature of the environmement is greater than ⅓ ?
If white plays the white "a" black "b" exchange white must then play in the environment and it is black turn. The point is the following : black is very happy with the previous white "a" black "b" exchange because it looks like black has herself played black "b" white "a" exchange which is quite good news for black.
That means that the previous white "a" black "b" exchange gains nothing to white and this exchange can even be considered bad because white has lost a potential ko threat.
With this analyse, unless you want to play here as a ko threat, you have to avoid playing in the area if the temperature of the environment is greater than ⅓.
White must wait for a temperature less or equal to ⅓ before playing in the area. In that case, after the white "a" black "b" exchange white will continue by connecting the ko (it is exactly what happenned in the game).
Eventually this white "a" black "b" exchange looks like a reversible play and we can verify that point by the following difference game:

Click Here To Show Diagram Code

[go]$$W
$$ -----------------
$$ | . X . X . O O O X |
$$ | X O X X . O O X . |
$$ | O O O X . O X X X |
$$ | . . . . . . . . . |
$$ | . . . . . . . . . |
$$ | . . . . . . . . . |
$$ | . . . . . . . . . |
$$ | . . . . . . . . . |
$$ -----------------[/go]

the two positions are equivalent and we can conclude that the white "a" black "b" exchange reverses for both players.
Finally the initial position is equivalent to a simple ko with a score -⅔ and a miai value ⅓.
The only difference is the following : if the temperature of the environment is between ¹/₃ and ⁷/₉ then white has here a ko threat.

_________________
The Adkins Principle:
At some point, doesn't thinking have to go on?
— Winona Adkins

Visualize whirled peas.

Everything with love. Stay safe.

I not only agree that the count after is -1 ⁴/₉ but that was exactly my calculation.

Click Here To Show Diagram Code

[go]$$Bc
$$ -----------------
$$ | . X 1 X . . . |
$$ | X O X X . . . |
$$ | O O O X . . . |
$$ | . . . . . . . |
$$ | . . . . . . . |
$$ | . . . . . . . |
$$ | . . . . . . . |
$$ -----------------[/go]

In addition, after the count of the position is -¹/₃

That was my first calculation and my first conclusion : if white plays first he will reach a position counted -1 ⁴/₉ and if black plays first she will reach a position counted -¹/₃ then the original position should be counted -⁸/₉ with a miai value of ⁵/₉.

In fact this result is not correct because we have now to take into account gote/sente situation.
When white plays first it seems he gains ⁵/₉ but now a following move will gain ⁷/₉. That means that white is sente.
In the other hand when black plays first it seems she gains ⁵/₉ and a following move will gain ¹/₃. That means that is gote.
Finally I count the initial position -²/₃ with a black reverse sente move equal to ¹/₃.
OC, the exchange gains nothing because it is a "normal" sente move which can act as a ko threat if temperature in the environment is between ¹/₃ and ⁷/₉.
Do you agree Bill?

Based upon the assumption that the position is gote.



would gain ⁵/₉ if it were gote, but it is sente-like, so it gains ⁷/₉ = -⅔ + 1 ⁴/₉. (It is not sente because the sente sequence, - , does not lower the original temperature.)



And it gains only ⅓ = -⅓ + ⅔.



Like a normal sente, - gains nothing in terms of points, and can be a ko threat.

_________________
The Adkins Principle:
At some point, doesn't thinking have to go on?
— Winona Adkins

Visualize whirled peas.

Everything with love. Stay safe.

Click Here To Show Diagram Code

[go]$$Wc
$$ -----------------
$$ | . X . X . . . |
$$ | X O X X . . . |
$$ | O O O X . . . |
$$ | . . . . . . . |
$$ | . . . . . . . |
$$ | . . . . . . . |
$$ | . . . . . . . |
$$ -----------------[/go]

We saw that if temperature of the environment is greater than ⅓ then black cannot play in the area and white can play in sente if temperature is not greater than ⁷/₉.
What if temperature is lower or equal to ⅓ ?

Click Here To Show Diagram Code

[go]$$Wc White to play
$$ -----------------
$$ | 1 X 2 X . . . |
$$ | X O X X . . . |
$$ | O O O X . . . |
$$ | . . . . . . . |
$$ | . . . . . . . |
$$ | . . . . . . . |
$$ | . . . . . . . |
$$ -----------------[/go]

connect
in the environment
white reaches in gote a position counted -1.

Click Here To Show Diagram Code

[go]$$Bc Black to play
$$ -----------------
$$ | 2 X 1 X . . . |
$$ | X O X X . . . |
$$ | O O O X . . . |
$$ | . . . . . . . |
$$ | . . . . . . . |
$$ | . . . . . . . |
$$ | . . . . . . . |
$$ -----------------[/go]

in the environment
connect
in the environment

Comparing the two results the difference is roughly the temperature of the environment. What does that mean? It appears that white interest is to wait as far as possible before playing in the area. Consequently the expecting sequence is the last diagram with black playing first in the area.
This is an unexpected result : white must avoid the exchange (except for using this sequence as a ko threat) and black must play the exchange in sente as soon as the temperature of the environment drops to ⅓.
Here is an example:

Click Here To Show Diagram Code

[go]$$Wc white to play
$$ -----------------
$$ | b X . X . X . |
$$ | X O X X X X X |
$$ | O O O O O O O |
$$ | . . O O O . . |
$$ | O O O O O O O |
$$ | O X X X X X X |
$$ | a O X . X X . |
$$ -----------------[/go]

white to play must play "a" to win. Playing "b" in sente will be a mistake.

It is a rather strange result : the white sente exchange is bad unless it is used as a ko threat. The expected play is the sente exchange as soon as temperature drops to ⅓.
Very interesting indeed.

It means that you compared sequences with a different number of moves.

Let a play in the environment gain t points. Then the result after 4 plays in the first diagram is -1 + t. And the result after 4 plays in the second diagram is also -1 + t. All same same. As I indicated above, the thermograph of this ko position with no ko threats is the line v = -1 + t at or below temperature ⅓.



Above temperature ⅓ there is the ko threat matter which you have discussed. Below temperature ⅓ the inclined mast indicates that White should wait until the ambient temperature reaches 0, if possible, and Black should make the play as early as possible. (In real life there are no plays on the go board between temperature ⅓ and temperature 0 -- although I have constructed one or two -- so the question is moot.)



Actually, it is more general than that. As a rule it is better to fill a ko at a certain temperature than to take a ko of the same size.



Yes, it is very interesting. But it is not unusual.

_________________
The Adkins Principle:
At some point, doesn't thinking have to go on?
— Winona Adkins

Visualize whirled peas.

Everything with love. Stay safe.

It seems we have now a common understanding.

Click Here To Show Diagram Code

[go]$$Wc
$$ -----------------
$$ | a X b X . . . |
$$ | X O X X . . . |
$$ | O O O X . . . |
$$ | . . . . . . . |
$$ | . . . . . . . |
$$ | . . . . . . . |
$$ | . . . . . . . |
$$ -----------------[/go]

A white move at "a" not only gains nothing but may be a mistake and must be avoid unless white can use this move as a ko threat between temperature 1/3 and 7/9. The expected local sequence shoud be the black sente exchange black b white a which must occur as soon as temperature drops to 1/3.