OK. Tryss worked out the answer.

I am going to add some discussion, and explain why these positions and plays are gote.
- Click Here To Show Diagram Code
[go]$$B
$$ ----------------------
$$ | a O . O . O . O . X .
$$ | . O X X X X X X X X .
$$ | . O 1 O . O . O . X .
$$ | . O X X X X X X X X .
$$ | b O 2 O . O . O . X .
$$ | . O X X X X X X X X .
$$ | . O 2 O 3 O . O . X .
$$ | . O X X X X X X X X .
$$ | c O 2 O 4 O . O . X .
$$ | . O X X X X X X X X .
$$ | . O 2 O 4 O 5 O . X .
$$ | . O X X X X X X X X .
$$ | . O 2 O 4 O 6 O . X .
$$ | . O X X X X X X X X .
$$ | . . . . . . . . . . .[/go]
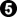
and

are each gote, and provide the final local score, 3 pts. for Black after
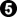
and 0 pts. after

So for the average value of "c" we take the average of those two two scores, or 1½ pts. for Black, on average.
Similarly, for the average value of "b" we can take the average of the value after

(6 pts. for Black) and the value after

(1½ pts. for Black). That gives us an average value of 3¾ pts. for Black.
Likewise, for the average value of "a" we can take the average of the value after

(9 pts. for Black) and the value after

(3¾ pts. for Black). That gives us an average value of 6⅜ pts. for Black.
Having figured the values of the different positions, let's go back and figure how much each play gains, on average. As we have seen, all the values are in terms of Black territory.
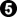
starts from a position worth 1½ pts. on average and moves to a position worth 3 pts., for an average gain of 1½ pts.

starts from a position worth 1½ pts. on average and move to a position worth 0, also for an average gain of 1½ pts. Each player's move gains the same (on average).

starts from a position worth 3¾ pts. on average and moves to a position worth 6 pts., for an average gain of 2¼ pts.

starts from a position worth 3¾ pts. on average and moves to a position worth 1½ pts. on average, also for an average gain of 2¼ pts., as expected.


starts from a position worth 6⅜ pts. on average and moves to a position worth 9 pts., for an average gain of 2⅝ pts.

starts from a position worth 6⅜ pts. on average and moves to a position worth 3¾ pts. on average, also for an average gain of 2⅝ pts.
Note: Go players usually don't talk about these value as averages, but they are, and so to be careful I am doing so.
We say that all of the non-final positions, "a", "b", and "c" are gote, and all of the moves

to

are gote. How come?
Well,
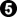
and

are obviously gote, because they are single plays that move to a scorable position. So are

and

. What about

and

?

gains on average 2¼ pts., while
gains on average 1½ pts. This method of evaluating plays is helpful because as a rule the best gote play is one that gains the most, on average. Normally there will be a gote play elsewhere on the board that gains less than 2¼ pts. (on average) and more than 1½ pts. (on average) for Black. In that case, then, Black will usually do better to make that play than
, and so White can play

with gote. Sometimes
will be Black's best play after

, and so

will be played with sente. However, we still classify

as gote.
You may verify that

gains more than

, on average, and so we classify

as gote, too.

Note that the difference in average gains between

and

is only ⅜ of a point, so
may well be the best reply to

and then White may play

with sente. That does not alter the classification, however.




