There are a lot of points that Black could improve but let's concentrate on one. When White played 1 in the diagram below (83 in the game), Black should absolutely want to separate White into the two groups of marked stones shown below if at all possible. Of course if Black recognizes the threat of a Black play at P8 as shown by Bill above, it is much more powerful. But even without that, fundamentally we want to keep the upper White stones as targets for attacking. How does Black tell whether this is possible?
- Click Here To Show Diagram Code
[go]$$Wcm1 Keeping White Separated
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . X . . . |
$$ | . . . . . . . . . . . . . . O X O O . |
$$ | . . . . . O . . X . . X O . . X O . O |
$$ | . . . X . . . . . , . . X . . X X O O |
$$ | . . . . . . . . . . . . . X X . . X X |
$$ | . . . . . . . . . . . . Q X Q X X . . |
$$ | . . . . . . . . . . . Q . Q Q Q . . . |
$$ | . . . . . . . . . . . . . . . 2 X X . |
$$ | . . . . . . . . . . . Q X X X 1 . @ . |
$$ | . . . , . . . . . X X X @ @ . , @ @ . |
$$ | . . . . . . . . . . X @ . . @ . @ . . |
$$ | . . . . . . . . . . . . X . . @ X @ @ |
$$ | . . . . . . . . . . X X . . @ . X X X |
$$ | . . X . . . . . . . O O X X X . X . . |
$$ | . . . . . . . . . . . . O X . . X . . |
$$ | . . . X . . . . . , . . O X . X O . . |
$$ | . . . . . O . . . . O . . O X X O . . |
$$ | . . . . . . . . . . . . . O X O . O . |
$$ | . . . . . . . . . . . . . . X O . . . |
$$ ---------------------------------------[/go]
The most basic question is what happens if White cuts with

below? Black can respond with
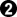
and just keep on pushing if White tries to keep the Black stones separated in turn. Notice that when the ataris run out and Black connects at
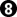
, the black stones have 6 liberties while the triangled white stones only have 3. That means that White has to go back and connect at

or everything has been meaningless up to now. However, when Black simply jumps to

White's stones are almost certainly captured.
- Click Here To Show Diagram Code
[go]$$Wcm1 Black can move out
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . X . . . |
$$ | . . . . . . . . . . . . . . O X O O . |
$$ | . . . . . O . . X . . X O . . X O . O |
$$ | . . . X . . . . . , . . X . . X X O O |
$$ | . . . . . . . . . . . . . X X . . X X |
$$ | . . . . . . . . . 0 . . O X Q X X . . |
$$ | . . . . . . . . . . . O 9 Q Q Q . . . |
$$ | . . . . . . . . . 6 4 2 8 . 1 X X X . |
$$ | . . . . . . . . 7 5 3 O X X X O . O . |
$$ | . . . , . . . . . X X X O O . , O O . |
$$ | . . . . . . . . . . X O . . O . O . . |
$$ | . . . . . . . . . . . . X . . O X O O |
$$ | . . . . . . . . . . X X . . O . X X X |
$$ | . . X . . . . . . . O O X X X . X . . |
$$ | . . . . . . . . . . . . O X . . X . . |
$$ | . . . X . . . . . , . . O X . X O . . |
$$ | . . . . . O . . . . O . . O X X O . . |
$$ | . . . . . . . . . . . . . O X O . O . |
$$ | . . . . . . . . . . . . . . X O . . . |
$$ ---------------------------------------[/go]
So White cannot cut Black and plays

below to force Black to connect. Black could just play P12 in gote but that lets White get the first move at the top (we will continue to assume that Black does not recognize the P8 threat here). Is there more that Black can do? Note that the three marked Black stones still have 3 liberties. Can we use this? First we can play the atari at
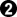
, forcing White to connect. But then we can also play
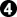
. The two marked white stones have only 2 liberties so this is a real threat that White needs to answer. White is better at reading than Black and answers at

, saving the right-side stones. However, Black gets to atari with

and again with
. This move is key. Black threatens to cut at Q9 so White has to answer. However, now Black is already connected since he can play either R11 or P12. As a result, Black gets to play first on the outside with something like

.
- Click Here To Show Diagram Code
[go]$$Wcm1 Black keeps sente to attack on the top
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . X . . . |
$$ | . . . . . . . . . . . . . . O X O O . |
$$ | . . . . . O . . X . . X O . . X O . O |
$$ | . . . X . . . . . , . . X . . X X O O |
$$ | . . . . . . . . . . . . . X X . . X X |
$$ | . . . . . . . . . . . . O X O X X . . |
$$ | . . . . . . . . . 0 . O . O O O . . . |
$$ | . . . . . . . . . . . 3 1 . . X X X . |
$$ | . . . . . . . . . . 2 O # # # O . O . |
$$ | . . . , . . . . . X X X Q Q 4 8 O O . |
$$ | . . . . . . . . . . X O 6 7 O 9 O . . |
$$ | . . . . . . . . . . . . X 5 . O X O O |
$$ | . . . . . . . . . . X X . . O . X X X |
$$ | . . X . . . . . . . O O X X X . X . . |
$$ | . . . . . . . . . . . . O X . . X . . |
$$ | . . . X . . . . . , . . O X . X O . . |
$$ | . . . . . O . . . . O . . O X X O . . |
$$ | . . . . . . . . . . . . . O X O . O . |
$$ | . . . . . . . . . . . . . . X O . . . |
$$ ---------------------------------------[/go]
In a five-stone game White may be able to live here. Black should not mind as long as the White stones are contained and Black can build walls on the outside. Imagine that White makes two eye for the top group. That will be two points for White at the top, three points on the right, and three points in the top right corner (as Bill showed, Black can kill the bottom right corner). Black has more territory than that in the upper right and the right side group. So now can Black make more territory on the rest of the board than White can make on the bottom? It looks like a fun challenge for Black.
PS: In the last diagram above it is actually better for Black to play
first without
and

. Can you see why? It has to do with Black's shortage of liberties.
_________________
Dave Sigaty"Short-lived are both the praiser and the praised, and rememberer and the remembered..."
- Marcus Aurelius; Meditations, VIII 21



