Gérard TAILLE wrote:
Bill Spight wrote:
However, if Move1 has a miai value, t1 <= 1, and Move2 has a miai value, t2 < t1, then Move1 dominates Move2, with the ko caveat. This is shown in "Mathematical Go" via the concept of chilling (See https://senseis.xmp.net/?Chilling ). Chilling is derived there, but the derivation uses aspects of CGT with which I am not familiar.
A great result of "Mathematical Go". Any clue to prove this result which allows to trust and use chilled go?
I understood you are not familiar with this point of "Mathematical Go" but you might have the main idea of the proof (?)
Regular go players are used to ignoring dame in territory scoring. For instance, in your recent example, they might write the sum of games this way:
{2|0} + {1|0}
But for these two games, {2|0} > {1|0}, i.e., {2|0} - {1|0} > 0, i.e.,
{2|0} + {0|-1} > 0
1) Black first will play in the left hand game and then White will answer in the right hand game, for a score of 2 - 1 = 1 > 0. Black wins.
2) White first will also play in the left hand game and then Black will reply in the right hand game, for a score of 0 + 0 = 0, with White to play. Black wins this way also.
Without the dame {2|0} and {1|0} are not incomparable, which justifies the ordinary go player's practice of ignoring the dame.
In CGT we write * (star) for a dame. It turns out, as you may verify, {1|0} is impossible on the go board. You either have {1|*} or {1*|0}. (1* means 1 plus a dame.) Likewise, you either have {2|0} or {2*|*}. This fact allows us to restore the dame to {1|0}, getting {1*|0} or {1|*} depending upon the context of the whole board. So ignoring the dame does not lose any significant information. (The result by area scoring will remain the same when any ignored dame are restored.) Ignoring the dame justifies chilling, because the strict ordering of chilled go is the same as the ordering before chilling when the dame are ignored. IOW, correct play at chilled go is also correct at regular go, up to a dame, with the ko caveat.
Edit: Why a dame? Because an even number of dame add to zero. I think that chilling would not work if regular go had fractional scores on the board. Ignoring the dame would lose significant information that could not be restored. (Edit: For instance, ignoring dame would change 3 points without capturing to 2½ points without capturing.
) Restoring the dame depends upon the parity of the empty points on the board plus prisoners.When I first read Mathematical Go I got it that chilling depends upon ignoring dame, which I was doing, anyway. So what's the problem?
is at 2, 
at 1 plays to 0. This means that the White connection dominates the intrusion into the short corridor.
prisoner.
is at 2,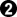 
at 1 plays to 0. This means that the Black capture dominates closing off the short corridor.
)