Late Halloween problem

Bill Spight · #1

This one may be a little spooky. :shock:

White to play.

EdLee · #2

Hi Bill

Bill Spight · #3

EdLee wrote:

Hi Bill

Hi, Ed.

Hidden for no good reason.

EdLee · #4

Hi Bill

lightvector · #5

Solution attempt, but I didn't as thoroughly try to understand the situations involved as on past endgame problems, so I might be missing something.

First white takes the biggest move on the board (2 points?). Next, as far as I can tell all remaining situations are worth 1 point per move, so this is purely a fight to get the last move.

Click Here To Show Diagram Code: [go]$$Wc Biggest move first $$ --------------------- $$ | . O . . . O X . . | $$ | . O X O . O X . X | $$ | X O O O . O X . . | $$ | . . O X . O X X . | $$ | O X X O X O O O 1 | $$ | X . X O O O X X . | $$ | . X X O X X . X O | $$ | X X b O O X X . X | $$ | O a O . O O X X . | $$ ---------------------[/go]

The bottom left is "good for White" in that White has a choice of how to play. White plays 'a' to finish the situation and locally get the last 1 point move, and 'b' to leave another 1 point move. By contrast, black only has one move 'b' to finish the situation. This gives White a lot of control over whether the final number of 1 point moves exchanged is odd or even and therefore whether White gets the last one.

The top right is also good for white because has a sneaky tesuji:

Click Here To Show Diagram Code: [go]$$Wc Sneaky tesuji $$ --------------------- $$ | . O . . . O X 2 . | $$ | . O X O . O X 1 X | $$ | X O O O . O X T 3 | $$ | . . O X . O X X S | $$ | O X X O X O O O O | $$ | X . X O O O X X . | $$ | . X X O X X . X O | $$ | X X . O O X X . X | $$ | O . O . O O X X . | $$ ---------------------[/go]

And now black must play at the triangled point rather than the squared point because otherwise he dies in an unwinnable ko. White takes gote, but reduces black by one extra point. Because white has the choice of the sente push or this gote extra point, this situation is also good for white and gives white control over who gets the last move.

The upper left situation confuses me a lot, so I'm not going to try to characterize it, instead I'll just look at some whole board lines. In general, White wants to leave unfinished the upper right and the lower left as long as possible to leave open the options of which variations to choose, while black would prefer to finish them to take that away.

So let's say Black takes the lower left. Some playing around suggests White responds like this and will win by 1 point:

Click Here To Show Diagram Code: [go]$$cb Black lower left first - White wins? $$ --------------------- $$ | . O . . . O X . . | $$ | 4 O X O . O X . X | $$ | X O O O . O X . . | $$ | 3 2 O X . O X X a | $$ | O X X O X O O O O | $$ | X . X O O O X X b | $$ | . X X O X X . X O | $$ | X X 1 O O X X . X | $$ | O . O . O O X X . | $$ ---------------------[/go]

Now, if Black connects, White takes a and then b. If Black takes a, White captures and leaves a situation that is miai with b. If Black takes b, White captures and leaves a situation that is miai with the tesuji in the upper right.

If Black takes the upper right first it's almost the same thing but with the moves in the upper right swapped with those of the lower left:

Click Here To Show Diagram Code: [go]$$cb Black upper right first - similar ideas? $$ --------------------- $$ | . O . . . O X . . | $$ | 4 O X O . O X . X | $$ | X O O O . O X . . | $$ | 3 2 O X . O X X 1 | $$ | O X X O X O O O O | $$ | X . X O O O X X b | $$ | . X X O X X . X O | $$ | X X a O O X X . X | $$ | O c O . O O X X . | $$ ---------------------[/go]

Now if Black connects, White a leaves a situation miai with b. If Black takes a, White captures and leaves a situation miai with b. If Black takes b, White captures and leaves a situation miai with c.

And if black plays in the upper left first, White is happy to oblige and finish the upper left position, and then easily uses the two advantageous positions to secure the last move. For example:

Click Here To Show Diagram Code: [go]$$cb Black upper left first - white wins $$ --------------------- $$ | . O . . . O X . . | $$ | 1 O X O . O X . X | $$ | X O O O . O X . 5 | $$ | 3 2 O X . O X X 4 | $$ | O X X O X O O O O | $$ | X . X O O O X X . | $$ | . X X O X X . X O | $$ | X X 6 O O X X . X | $$ | O . O . O O X X . | $$ ---------------------[/go]

Click Here To Show Diagram Code: [go]$$cb Black upper left another variation - white wins $$ --------------------- $$ | . O . . . O X . . | $$ | 2 O X O . O X . X | $$ | X O O O . O X . . | $$ | 4 1 O X . O X X 5 | $$ | O X X O X O O O O | $$ | X . X O O O X X 6 | $$ | . X X O X X . X O | $$ | X X 3 O O X X . X | $$ | O . O . O O X X . | $$ ---------------------[/go]

Bill Spight · #6

lightvector wrote:

Solution attempt, but I didn't as thoroughly try to understand the situations involved as on past endgame problems, so I might be missing something.

First white takes the biggest move on the board (2 points?). Next, as far as I can tell all remaining situations are worth 1 point per move, so this is purely a fight to get the last move.

Click Here To Show Diagram Code: [go]$$Wc Biggest move first $$ --------------------- $$ | . O . . . O X . . | $$ | . O X O . O X . X | $$ | X O O O . O X . . | $$ | . . O X . O X X . | $$ | O X X O X O O O 1 | $$ | X . X O O O X X . | $$ | . X X O X X . X O | $$ | X X b O O X X . X | $$ | O a O . O O X X . | $$ ---------------------[/go]

The bottom left is "good for White" in that White has a choice of how to play. White plays 'a' to finish the situation and locally get the last 1 point move, and 'b' to leave another 1 point move. By contrast, black only has one move 'b' to finish the situation. This gives White a lot of control over whether the final number of 1 point moves exchanged is odd or even and therefore whether White gets the last one.

The top right is also good for white because has a sneaky tesuji:

Click Here To Show Diagram Code: [go]$$Wc Sneaky tesuji $$ --------------------- $$ | . O . . . O X 2 . | $$ | . O X O . O X 1 X | $$ | X O O O . O X T 3 | $$ | . . O X . O X X S | $$ | O X X O X O O O O | $$ | X . X O O O X X . | $$ | . X X O X X . X O | $$ | X X . O O X X . X | $$ | O . O . O O X X . | $$ ---------------------[/go]

And now black must play at the triangled point rather than the squared point because otherwise he dies in an unwinnable ko. White takes gote, but reduces black by one extra point. Because white has the choice of the sente push or this gote extra point, this situation is also good for white and gives white control over who gets the last move.

The upper left situation confuses me a lot, so I'm not going to try to characterize it, instead I'll just look at some whole board lines. In general, White wants to leave unfinished the upper right and the lower left as long as possible to leave open the options of which variations to choose, while black would prefer to finish them to take that away.

So let's say Black takes the lower left. Some playing around suggests White responds like this and will win by 1 point:

Click Here To Show Diagram Code: [go]$$c Black lower left first - White wins? $$ --------------------- $$ | . O . . . O X . . | $$ | 4 O X O . O X . X | $$ | X O O O . O X . . | $$ | 3 2 O X . O X X a | $$ | O X X O X O O O O | $$ | X . X O O O X X b | $$ | . X X O X X . X O | $$ | X X 1 O O X X . X | $$ | O . O . O O X X . | $$ ---------------------[/go]

Now, if Black connects, White takes a and then b. If Black takes a, White captures and leaves a situation that is miai with b. If Black takes b, White captures and leaves a situation that is miai with the tesuji in the upper right.

If Black takes the upper right first it's almost the same thing but with the moves in the upper right swapped with those of the lower left:

Click Here To Show Diagram Code: [go]$$c Black upper right first - similar ideas? $$ --------------------- $$ | . O . . . O X . . | $$ | 4 O X O . O X . X | $$ | X O O O . O X . . | $$ | 3 2 O X . O X X 1 | $$ | O X X O X O O O O | $$ | X . X O O O X X b | $$ | . X X O X X . X O | $$ | X X a O O X X . X | $$ | O c O . O O X X . | $$ ---------------------[/go]

Now if Black connects, White a leaves a situation miai with b. If Black takes a, White captures and leaves a situation miai with b. If Black takes b, White captures and leaves a situation miai with c.

And if black plays in the upper left first, White is happy to oblige and finish the upper left position, and then easily uses the two advantageous positions to secure the last move. For example:

Click Here To Show Diagram Code: [go]$$c Black upper left first - white wins $$ --------------------- $$ | . O . . . O X . . | $$ | 1 O X O . O X . X | $$ | X O O O . O X . 5 | $$ | 3 2 O X . O X X 4 | $$ | O X X O X O O O O | $$ | X . X O O O X X . | $$ | . X X O X X . X O | $$ | X X 6 O O X X . X | $$ | O . O . O O X X . | $$ ---------------------[/go]

Click Here To Show Diagram Code: [go]$$c Black upper left another variation - white wins $$ --------------------- $$ | . O . . . O X . . | $$ | 2 O X O . O X . X | $$ | X O O O . O X . . | $$ | 4 1 O X . O X X 5 | $$ | O X X O X O O O O | $$ | X . X O O O X X 6 | $$ | . X X O X X . X O | $$ | X X 3 O O X X . X | $$ | O . O . O O X X . | $$ ---------------------[/go]

Bill Spight · #7

lightvector solved the problem, as usual. :clap:

Nobody else posted an attempt, so I don't see much point in hiding this.

Click Here To Show Diagram Code: [go]$$W Correct play $$ ------------------- $$ | . O . . . O X . . | $$ | 5 O X O . O X . X | $$ | X O O O . O X . . | $$ | 4 3 O X . O X X 2 | $$ | W X X O X O O O 1 | $$ | X . X O O O X X 9 | $$ | . X X O X X . X O | $$ | X X 6 O O X X . X | $$ | O . O . O O X X . | $$ -------------------[/go]

at

at 4

This diagram shows technically correct play. White gets the last move and wins by 1 point. If White deviates, Black can make jigo.

Click Here To Show Diagram Code: [go]$$W White failure $$ ------------------- $$ | . O . . . O X . . | $$ | 7 O X O . O X . X | $$ | X O O O . O X . 2 | $$ | 6 5 O X . O X X 1 | $$ | W X X O X O O O 3 | $$ | X . X O O O X X 8 | $$ | . X X O X X . X O | $$ | X X 4 O O X X . X | $$ | O . O . O O X X . | $$ -------------------[/go]

at

at 6

The hane, :b1:

, holds Black to 4 points in the corner, but then Black can get the last play for jigo.

One problem with this problem is that the failure option for White is not very intuitive. OTOH, one thing I like about it is that each independent region is a little tricky.

More analysis later.

Bill Spight · #8

As with so many of my problems, this one ultimately comes down to getting the last move that gains one point. Let's take a look at different areas of the board from that perspective.

Click Here To Show Diagram Code: [go]$$Wc Correct play $$ ------------------- $$ | . O . . . O X . . | $$ | . O X O . O X . X | $$ | X O O O . O X . . | $$ | . b O X . O X X 2 | $$ | O X X O X O O O 1 | $$ | X . X O O O X X a | $$ | . X X O X X . X O | $$ | X X . O O X X . X | $$ | O . O . O O X X . | $$ -------------------[/go]

After

a move at "a" will gain one point for either Black or White. The bottom right goes into the undecided or fuzzy column.

However, Black will get the last play in the top left corner.

Click Here To Show Diagram Code: [go]$$Wc White first, Black last $$ ------------------- $$ | . O . . . O X . . | $$ | 3 O X O . O X . X | $$ | X O O O . O X . . | $$ | 2 1 O X . O X X X | $$ | W X X O X O O O O | $$ | X . X O O O X X . | $$ | . X X O X X . X O | $$ | X X . O O X X . X | $$ | O . O . O O X X . | $$ -------------------[/go]

fills at

Click Here To Show Diagram Code: [go]$$Bc Black first and last $$ ------------------- $$ | . O . . . O X . . | $$ | 2 O X O . O X . X | $$ | X O O O . O X . . | $$ | 3 1 O X . O X X X | $$ | O X X O X O O O O | $$ | X . X O O O X X . | $$ | . X X O X X . X O | $$ | X X . O O X X . X | $$ | O . O . O O X X . | $$ -------------------[/go]

If the top left corner is the last place on the board left to play, then Black will get the last play. In the fight to get the last play, we say that it is positive for Black. OC, Black will avoid playing there, and by the same token White will wish to play there.

Now let's look at the bottom left.

Click Here To Show Diagram Code: [go]$$Bc Black first and last $$ ------------------- $$ | . O . . . O X . . | $$ | . O X O . O X . X | $$ | X O O O . O X . . | $$ | . . O X . O X X X | $$ | O X X O X O O O O | $$ | X . X O O O X X . | $$ | . X X O X X . X O | $$ | X X 1 O O X X . X | $$ | W . O . O O X X . | $$ -------------------[/go]

captures the :wc:

stone, leaving miai in the corner.

Click Here To Show Diagram Code: [go]$$Wc White first and last $$ ------------------- $$ | . O . . . O X . . | $$ | . O X O . O X . X | $$ | X O O O . O X . . | $$ | . . O X . O X X X | $$ | O X X O X O O O O | $$ | X . X O O O X X . | $$ | . X X O X X . X O | $$ | X X 2 O O X X . X | $$ | W 1 O 3 O O X X . | $$ -------------------[/go]

saves the

stone.

Since each player can play first and get the last play, the bottom left is fuzzy, too.

More analysis to come.

Bill Spight · #9

Let's take a look a little later in the game.

Click Here To Show Diagram Code: [go]$$Wc Correct play $$ ------------------- $$ | . O . . . O X . . | $$ | 5 O X O . O X . X | $$ | X O O O . O X . . | $$ | 4 3 O X . O X X 2 | $$ | O X X O X O O O 1 | $$ | X . X O O O X X . | $$ | . X X O X X . X O | $$ | X X . O O X X . X | $$ | O . O . O O X X . | $$ -------------------[/go]

Leaving

Click Here To Show Diagram Code: [go]$$Bc Result $$ ------------------- $$ | . O . . . O X . . | $$ | O O X O . O X . X | $$ | B O O O . O X . . | $$ | B O O X . O X X X | $$ | C X X O X O O O O | $$ | X . X O O O X X . | $$ | . X X O X X . X O | $$ | X X . O O X X . X | $$ | O . O . O O X X . | $$ -------------------[/go]

A couple of things to note about this position: First, White has played with gote in the top left, but it is still positive for Black. The resulting shape (marked) is a familiar one, called an UP. (See http://senseis.xmp.net/?UP and linked pages.) In an UP, Black to play can take the last play or White to play can play to a simple fuzzy position called a STAR. (See http://senseis.xmp.net/?STAR and linked pages.) The position on the right side and the position after White captures the :bc:

stones are examples of STAR. Since White has to take gote to reach UP, the original position in the top left corner is more positive that UP. In fact, it is called DOUBLE UP STAR. (See http://senseis.xmp.net/?CorridorInfinitesimals)

Second, even though Black plays first in this position, in spite of the fact that the top left is positive for Black, White gets the last play. That means that the rest of the board is negative for Black (positive for White), in fact, at least as negative as UP is positive. And that means that two fuzzy positions add up to a negative position. :shock:

Most peculiar, Mama!

We have already seen, without comment, how two fuzzy positions can add up to a non-fuzzy position. See next diagram.

Click Here To Show Diagram Code: [go]$$Bcm6 Miai $$ ------------------- $$ | . O . . . O X . . | $$ | O O X O . O X . X | $$ | B O O O . O X . . | $$ | B O O X . O X X X | $$ | 2 X X O X O O O O | $$ | X . X O O O X X . | $$ | . X X O X X . X W | $$ | X X 1 O O X X . X | $$ | O . O . O O X X . | $$ -------------------[/go]

After

the capture of the :wc:

stone and the capture of the :w7:

stone are miai. Both local positions are fuzzy, but because of miai, they add up to the same thing, 1 net point for Black, no matter who plays first. We say that two STARs add up to 0.

It turns out that after :w5:

the UP in the top left is miai with the two fuzzy positions on the rest of the board.

Click Here To Show Diagram Code: [go]$$Wc Miai $$ ------------------- $$ | . O . . . O X . . | $$ | O O X O . O X . X | $$ | B O O O . O X . . | $$ | B O O X . O X X X | $$ | 1 X X O X O O O O | $$ | X . X O O O X X . | $$ | . X X O X X . X W | $$ | X X 2 O O X X . X | $$ | O . O . O O X X . | $$ -------------------[/go]

White to play will capture the :bc:

stones and then Black will play :b2:

to settle the bottom left corner. The result is the same as when Black plays first. That means that the two positions in the bottom left corner and right side add up to the negative of UP, which is DOWN. In fact, the bottom left corner is worth DOWN plus STAR, or DOWN STAR, which, added to the STAR on the right, yields DOWN.

More to come!

Bill Spight · **#10**

Bill Spight wrote:

Click Here To Show Diagram Code: [go]$$W Correct play $$ ------------------- $$ | . O . . . O X . . | $$ | 5 O X O . O X . X | $$ | X O O O . O X . . | $$ | 4 3 O X . O X X 2 | $$ | W X X O X O O O 1 | $$ | X . X O O O X X 9 | $$ | . X X O X X . X O | $$ | X X 6 O O X X . X | $$ | O . O . O O X X . | $$ -------------------[/go]

at

at 4

This diagram shows technically correct play.

Why do I make that claim?

Well, :w1:

is correct, at least if the rest of the play is.

I will defend later. :w3:

and

play where Black is positive, which is correct. What about :b6:

, though? Why not play at 9? OC, we could read it out, but Black loses, anyway. Why is :b6:

technically correct? After all, both plays gain just a much.

To answer that question we can compare the two plays with a difference game. (See http://senseis.xmp.net/?DifferenceGame )

Click Here To Show Diagram Code: [go]$$Bc Mirror $$ ------------------- $$ | X . X . X . X . X | $$ | O O . X X X X O O | $$ | . O O . . . . O . | $$ | . . . , . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . X X . . . . X . | $$ | X X . O O O O X X | $$ | O . O . O . O . O | $$ -------------------[/go]

The question is whether Black should capture the White stone in the bottom left corner or the White stone on the right side. To set up the difference game, for convenience I have moved the position on the right side to the bottom right corner. That is not necessary, but it makes the setup easier. Then I have mirrored the bottom position on the top. In the difference game play is restricted to the regions of interest, the bottom two files and the top two files. The rest is no man's land. Mirroring sets up a miai which yields jigo, no matter who plays first. The position is strictly even.

To compare the plays we let Black make one of the plays on one side of the board and White make the mirror of the other play. The order of plays does not matter.

Click Here To Show Diagram Code: [go]$$Bc Difference game $$ ------------------- $$ | X . X . X . X W . | $$ | O O . X X X X O O | $$ | . O O . . . . O . | $$ | . . . , . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . X X . . . . X . | $$ | X X B O O O O X X | $$ | O . O . O . O . O | $$ -------------------[/go]

White has one Black prisoner.

If the difference game is strictly even, then the moves are equivalent. If the player who plays first wins the game, then we cannot say which move is better. That depends upon the rest of the board in each game. But if one player can win the difference game by playing first while getting at least a jigo by playing second, then the difference game favors that player, and that player's move is superior -- with one proviso. If there is a ko elsewhere in the real game, that can make the other play better.

In this case we know that the difference game is an UP, which is positive for Black. That means that Black will get the last play and win when she plays first, and will get the last play for jigo when White plays first. So the play in the bottom left corner is technically correct.

Out of curiosity, what about White's play? White has three choices: save the stone on the right side, save the stone in the bottom left corner, or make an eye in the bottom left corner, leaving the corner stone en prise. We cannot say which play is better in general, but we can show that saving the stone in the bottom left corner is technically incorrect. Saving the stone on the right side is superior.

----
Edit: I misspoke. :oops:

Actually, we can show that both the capture of the stone on the left and the stone on the right are inferior. Making a point on the bottom left and leaving both corners miai is technically correct. It does not require a difference game to show this.

Click Here To Show Diagram Code: [go]$$Wc Black gets the last play $$ | . . . . . . . . . | $$ | . X X . . . . X . | $$ | X X 2 O O O O X X | $$ | O . O . O . O 1 W | $$ -------------------[/go]

If

saves the

stone,

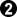
gets the last play. This is bad for White because the position is positive for White. It is wrong for White to let Black get the last play.

Click Here To Show Diagram Code: [go]$$Wc Black gets the last play $$ | . . . . . . . . . | $$ | . X X . . . . X . | $$ | X X 2 O O O O X X | $$ | O 1 O 3 O . O 4 O | $$ -------------------[/go]

The same is true for this line of play.

Click Here To Show Diagram Code: [go]$$Wc White gets the last play $$ | . . . . . . . . . | $$ | . X X . . . . X . | $$ | X X 1 O O O O X X | $$ | O . O . O . O . O | $$ -------------------[/go]

The only technically correct play is :w1:

.

----

Click Here To Show Diagram Code: [go]$$Bc Difference game 2 $$ ------------------- $$ | X B X B X . X . X | $$ | O O W X X X X O O | $$ | . O O . . . . O . | $$ | . . . , . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . X X . . . . X . | $$ | X X . O O O O X X | $$ | O . O . O . O W O | $$ -------------------[/go]

To set up the difference game White saves the stone in the bottom right and Black saves the mirror stone in the top left corner. Note that White finishes off the top left corner in sente. Those three plays form a unit. If Black allows White to capture three stones she is worse off than if she had not connected to the corner stone in the first place.

This difference game is a DOWN, which is good for White. So White's play of saving the stone on the right is superior, and saving the stone in the bottom left corner is inferior, and technically incorrect.

Edit: The setup of the difference game is wrong, because Black will not play in the top left corner after White plays in the bottom right corner.

Click Here To Show Diagram Code: [go]$$Wc Correction $$ ------------------- $$ | X . X . X . X . X | $$ | O O . X X X X O O | $$ | . O O . . . . O . | $$ | . . . , . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . X X . . . . X . | $$ | X X 2 O O O O X X | $$ | O . O . O . O 1 O | $$ -------------------[/go]

The result is an UP, which Black wins. That shows that :w1:

is incorrect.

Here is an edited SGF showing play in the difference games.

Even more to come!

Bill Spight · **#11**

Click Here To Show Diagram Code: [go]$$Wc Variation 1 $$ ------------------- $$ | . O . . . O X . . | $$ | . O X O . O X . X | $$ | X O O O . O X . . | $$ | . . O X . O X X . | $$ | O X X O X O O O 1 | $$ | X . X O O O X X . | $$ | . X X O X X . X O | $$ | X X 2 O O X X . X | $$ | O . O . O O X X . | $$ -------------------[/go]

I claim that :b2:

is technically incorrect, but how does play go if Black plays there?

Click Here To Show Diagram Code: [go]$$Wcm3 White failure $$ ------------------- $$ | . O . . . O X . . | $$ | 3 O X O . O X . X | $$ | X O O O . O X . 8 | $$ | 2 1 O X . O X X 7 | $$ | W X X O X O O O O | $$ | X . X O O O X X 4 | $$ | . X X O X X . X O | $$ | X X X O O X X . X | $$ | O . O . O O X X . | $$ -------------------[/go]

captures 2 stones at :wc:

takes back at 4

If White plays this way Black gets the last play for jigo. Where did White go wrong?

Click Here To Show Diagram Code: [go]$$Wcm9 Variation 2 $$ ------------------- $$ | . O . . . O X 2 . | $$ | O O X O . O X 1 X | $$ | . O O O . O X 4 3 | $$ | X O O X . O X X 5 | $$ | . X X O X O O O O | $$ | X . X O O O X X X | $$ | . X X O X X . X . | $$ | X X X O O X X . X | $$ | O . O . O O X X . | $$ -------------------[/go]

Black has captured 3 White stones, White has captured 2 Black stones

:w9:

is tesuji. Black cannot afford to play the ko, so White gets the last play to win by 1 point.

Note that White cannot afford to play :w9:

earlier.

may not be technically correct, but it gets jigo if White does not see :w9:

.

More later.

Bill Spight · **#12**

Well, it's already the day of the big match in Japan, so I'll be brief.

I made a misstatement in post #10 ( viewtopic.php?p=213101#p213101 ), and have corrected it.

I have claimed that :b2:

in the top right corner is technically correct. That claim depends upon Black not fighting the ko in the top right corner, which she obviously cannot do in the problem. But I also think that the ko is a picnic ko, and the standard textbook treatment of picnic kos is to avoid them. OC, if Black is komaster for the ko she can play it, but it is difficult for Black to be komaster.

Black has the option of playing in the bottom left corner, instead of in the top right corner. Let's compare the two plays with a difference game, even though difference games do not handle kos. I think that it will be instructive.

For convenience, I have moved the bottom left corner position to the bottom right corner.

Click Here To Show Diagram Code: [go]$$Bc Difference game setup $$ ------------------- $$ | . . O X . O X . . | $$ | O . O X . O X . X | $$ | . . O X . O X . . | $$ | . O O X . O X X B | $$ | X X X X . O O O O | $$ | . X . . . . . O . | $$ | X W . . . . . . O | $$ | . O O . . . X X . | $$ | X O . . . . . X O | $$ -------------------[/go]

For the setup we let Black play in the top right corner and White play in the bottom left corner. Both corners are settled, so the remaining areas of play are the top left corner and the bottom right corner. The rest is no man's land.

Click Here To Show Diagram Code: [go]$$Bc Black first wins $$ ------------------- $$ | . . O X . O X . . | $$ | O . O X . O X . X | $$ | 2 . O X . O X . . | $$ | 1 O O X . O X X X | $$ | X X X X . O O O O | $$ | . X . . . . . O . | $$ | X O . . . . . 3 O | $$ | . O O . . . X X . | $$ | X O . . . . . X O | $$ -------------------[/go]

is sente, threatening to kill the White group. After :w2:

protects,

gets the last play to win by 1 point.

Click Here To Show Diagram Code: [go]$$Wc Variation 1, jigo $$ ------------------- $$ | . . O X . O X . . | $$ | O . O X . O X . X | $$ | 3 . O X . O X . . | $$ | 2 O O X . O X X X | $$ | X X X X . O O O O | $$ | . X . . . . . O . | $$ | X O . . . . . 1 O | $$ | . O O . . . X X 4 | $$ | X O . . . . . X W | $$ -------------------[/go]

makes 1 point and threatens to save the :wc:

stone, but Black plays sente in the top left and then captures :wc:

for the last move and jigo.

Click Here To Show Diagram Code: [go]$$Wc Variation 2, jigo $$ ------------------- $$ | . 5 O X . O X . . | $$ | O 4 O X . O X . X | $$ | 6 7 O X . O X . . | $$ | 8 O O X . O X X X | $$ | X X X X . O O O O | $$ | . X . . . . . O 3 | $$ | X O . . . . . 2 O | $$ | . O O . . . X X 1 | $$ | X O . . . . . X O | $$ -------------------[/go]

is tesuji. :w7:

avoids the picnic ko, but allows Black to get the last play, for jigo.

Now, if we assume that Black avoids the picnic ko, then there is no ko, and the difference game is a good guide. However, in this case White can win the ko.

The ko fight is instructive.

Click Here To Show Diagram Code: [go]$$Wcm7 Ko fight $$ ------------------- $$ | 2 O O X . O X 4 . | $$ | O X O X . O X 3 X | $$ | X . O X . O X . 9 | $$ | 1 O O X . O X X X | $$ | X X X X . O O O O | $$ | 6 X . . . . . O O | $$ | X O . . . . . X O | $$ | 7 O O . . . X X O | $$ | B O . . . . . X O | $$ -------------------[/go]

,

take ko

White wins the ko because he has two large ko threats. :w9:

threatens to kill the Black corner outright, and :w15:

threatens ko for the corner. So it is certainly possible for White to be komaster.

However, look at Black's ko threat. All it threatens is to save the :bc:

stone and still make jigo. It is, I think, the fact that White needs large ko threats while Black needs only small threats that makes it hard for White to be komaster, and makes this a picnic ko. (Also the fact that it is a direct ko, neither an approach ko nor a 10,000 year ko, which also may have asymmetrical ko threats.)

Anyway, my claim that :b2:

is technically correct is certainly debatable.

----

BTW, I got the idea for this problem while playing around with the top right corner.

Click Here To Show Diagram Code: [go]$$B Black lives $$ ---------- $$ . O X 3 . | $$ . O X 2 1 | $$ . O X 5 4 | $$ . O X X . | $$ . O O O O | $$ . . . . . |[/go]

This kind of thing is one reason why I think that tsumego and yose benefit from being studied together.

Late Halloween problem

Who is online