More blather.

What is komi?
There is statistical komi and there is theoretical komi. Statistical komi is what we know for the 19x19 board. Given a group of players, each of whom plays Black or White half the time, statistical komi is the number of points that Black gives White which yields the odds of a Black win versus the odds of a White win that is closest to 50:50. Today we require a non-integer komi, to prevent ties. Theoretical komi is the best score that each player can guarantee for herself, given perfect play. We know theoretical komi for the 5x5 board. It is 24 pts. by territory scoring, 25 pts. by area scoring. And 24½ pts. for Button Go, BTW. Now, as the skill level of the players increases, statistical komi should converge to theoretical komi. Based upon statistics in the 1970s, theoretical komi for area scoring is probably 7 pts., and for territory scoring it is probably 6 or 7 pts. For AI trained on area scoring the statistical non-integer komi is 7½ pts.
In 1977 Terry Benson sent me an article to review about komi submitted to the AGA Journal based upon the statistics of 2800 Japanese professional games published by the Nihon Kiin, 1400 with a komi of 4½, and 1400 with a komi of 5½ (or 5 with White winning jigo). The author regarded it as "plain as a pikestaff" that theoretical komi under Japanese scoring was 7. When published, the article included a footnote by me pointing out that changing the komi might affect the play, something that John Fairbairn has also pointed out. That said, there was zero statistical evidence that changing the Japanese komi to 5½ from 4½ had affected the professionals' play. For the 1400 games played with 5½ komi a komi of 6½ gave the most even results, but the same was true for the games played with 4½ komi.

Based solely on the statistics of the 4½ komi games, komi could have been changed to 6½ without going through the 5½ komi stage.
So does komi affect opening play? Obviously the shift from 0 komi to 4½ komi did. But did the gradual change from 4½ komi to 6½ komi do so? I have not seen any evidence of that. OC, over four or five decades, opening play has changed, but I am unaware of any evidence that these changes affected the statistical distribution of final scores. Based upon statistics, Ing jumped to 7½ or 8 pts. komi for area scoring in the early 1980s. I am unaware of area scoring statistics.
What is an error? Errors are easy to define in terms of theoretical komi or, more generally, theoretical value. An error is a play that changes the result that, given perfect play, the player can guarantee negatively for that player. So if theoretical komi is 7 and after Black's first play, the theoretical value of the resulting position is 6, that play is an error. OC, in practice we do not really know either value for the 19x19 board.
But what if the actual komi is 4½? With perfect play Black will still win, so is it an error or not? There is a statistical answer. Even if Black should still win by perfect play, if the play reduces the chance that Black will win the game, it is an error. But we know that there are theoretical errors in many positions, that actually increase the chance that Black will in the game. Such plays make a small theoretical sacrifice in order to nail down Black's win.
Now bots, it seems, take the statistical point of view. Not that they base their plays entirely upon their estimates of the probability of winning the game, if at all (depending upon the bot, I think), but those estimates do affect their analysis, and in general they play so as to maximize their chance of winning the game. This fact was hyped a few years ago as bots thinking differently from humans. Well, they do, but that's not why.
Now, the bots' estimates are based upon erroneous play, not perfect play, but the erroneous play upon which they are based is their own, not the erroneous play of humans. Humans utilize the winrate estimates of the bots without really knowing what they mean, in a practical sense. A play that has a higher winrate than another when bot plays bot, may not have a higher winrate when human plays human. We may assume that a play with a higher winrate estimate is statistically better in human play, but we don't really know. However, the greater the difference between the winrate estimates of two plays, the more likely that the play with the worse winrate estimate is an error, however defined.
So when the Elf of the commentaries, which is only one bot, and not currently among the top bots, and a bot which produces relatively large winrate differences, reckons that Sakata's boshi loses more than 20% in winrate by comparison with an enclosure, I am inclined to think that the boshi is a human vs. human statistical error, and probably a theoretical error, as well. But we need to consult other, better bots, as well, to assess different plays and ideas.
My purpose in this series.
I think that books on the opening have to be rewritten for our AI era. The bots, OC, don't write books, they don't even offer explanations. But, just as the opening theory of the 20th century was largely based upon best play in the 19th century, I think that the opening theory of the 21st century will be largely based upon best play by bots. Science marches on.
It is up to us humans to come up with new explanations and ideas. Old ideas need to be discarded or modified. I doubt if the 21st century equivalent of Takagawa's
Fuseki Dictionary will be written by anybody now over 20 years old. I have proposed a new last play principle for the opening, which is not to get the last
Oba, but to occupy the last open corner. (OC, there are exceptions, but that's the rule.) I think it will hold up.
So I wanted to explore where the old textbooks may have it wrong, or where the ideas need to be modified. It was not my purpose to point out human mistakes. In fact, both humans and bots have rejected the 5-3 approach for
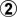
, despite the fact that it may not actually be a theoretical error.

And humans sometimes play it and win, even in 9 dan vs. 9 dan games. As for new theory, it helps to know what needs to be explained. That is where I am starting. The Elf commentaries provide a number of examples that can be found quickly.
I started emphasizing plays that, by comparison with its top choice, Elf reckons as losing several percentage points, because of my discussion with Sorin. He, quite reasonably, does not consider winrate estimates of human professional plays to be definitive. Fair enough. That's why I went looking for high winrate differences, which, in my educated judgement, have a good chance of indicating theoretical errors. Especially if other bots agree.




