Chen Zuyuan's summary of his history research is available in English on John Fairbairn's webpage:

http://www.gogod.co.uk/NewInGo/ChenZuyuan_1.htm
http://www.gogod.co.uk/NewInGo/ChenZuyuan_2.htm

I am still reading it for the first time and will have to read it several times to understand all. One thing is sure: The text is essential for anybody interested in rules history.

John, with which meaning do you use "string" in your final draft of the translation? Does it stand for "alive group" or "independently alive group" or "chain"?

Robert

1. It's not my website. It's GoGoD's.

2. I have no idea what definitions, if any, lie behind Mr Chen's choice of words. I don't see that it matters in this case. There is not enough surviving textual information to do more than make an informed judgement, which he is supremely well qualified to do. As he has said that he doesn't like to get into tedious nitpicking, I'm not going to ask him either (we have been enjoyably discussing ancient Chinese go poems instead). His aim was not to get into a debate but to provide education and entertainment for the ordinary western go reader. He is willing to provide more, so if it is appreciated it would be worth signifying.

Please note that my introduction says that the rigorous reader is specifically referred to his long articles and book. There's plenty more there to get your teeth into.

FWIW the Chinese phrase was 一块活棋 (but this is modern Chinese). As you can see, it specifically says live group.

3. In all honesty, I couldn't answer your question anyway. I have no idea what "alive group" or "independently alive group" mean. It's not proper English.

"...group that is alive" is proper English. Is there something else "alive group" could mean?

"Independently alive group" is confusing, because you need to know what the group is independent from and in what regard. But the problem isn't that it's ungrammatical.

_________________
Occupy Babel!

Common English might prefer "live group" instead of "alive group", I'd guess. When I say "alive group", I am im rules language mode because I have defined "alive" but not "live", so I use alive as a term. This language usage is independent of Chen's text though.

I am well aware that his text requires independent usage of terms derived from the historical originals rather than from present terms.

There is no need (yet) to define "alive" or "independently alive" or "group" for the sake of understanding his text. However, "string" appears to be dangerous usage here because, even after the stone scoring encore of filling in territories (aka "roads") it can happen that a group still consists of two, three or four strings (chains).

For an understanding of the text, it makes a difference whether it is "alive" or "independently alive" because group tax might have to be applied differently in "sekis".

It is easier to understand the text if Chinese to English translation difficulties can be identified first. Otherwise English-only readers face the difficulty of not knowing fur sure exactly which meaning was conveyed in the original historical findings.

My greatest other difficulty when reading the text so far is also a matter of Chinese to English translation (or maybe of Chen's difficulty to choose Chinese terms that allow unequivocal translation to Modern Rules English): at two or three places, I would understand the text more easily if "scoring" and "counting" were changed. OTOH, if these words should be chosen and translated accurately, then text interpretation will be more difficult for me.

Otherwise I am glad about the apparent accuracy of the translations and the preserving of the ancient Go terms.

This is a modern go term (and also a modern go rules term): Life is either independent (can be transformed to a two-eye-formation) or seki.

There are no examples of sekis in the very ancient games that survive so we can't know (except, tentatively, by inference from Japanese rules, as Chen has done). From memory, the earliest sekis in old Chinese games are from the Qianlong era, i.e. relatively recent. Group tax applied then and the effect of the seki was interesting, but (to me) only for about 10 seconds, so I've forgotten what the effect was.

hyperpape: "All mimsy were the borogoves" is grammatical but it ain't proper English. I infer you are not used yet to Robert re-inventing English words. See above. Beware the Jabberwock, my friend.

The Two Headed Dragon ( http://senseis.xmp.net/?TwoHeadedDragon ) is a case in point.



From what I have heard, in stone scoring days in China the group tax did not change the parity of the scores. IOW, there was no 1/2 zi tax. (Perhaps I have been misinformed.) But, as we know, some sekis do change the parity, as a group with a single defective eye may need it to live.



Well, John gave the Chinese term, which my online-stupid translation renders as "together live chess", and John clarifies as "live group".

Unless I am mistaken, in the historical examples discussed, none of the problematic applications of the group tax arise. And it is these specific examples where the scores are apparently territory scoring with a group tax. Chen thinks that they actually were what we might now call equivalence scoring, so that stone scoring was actually in use. (BTW, I disagree. Territory scoring with a group tax makes perfect sense.)

_________________
The Adkins Principle:
At some point, doesn't thinking have to go on?
— Winona Adkins

Visualize whirled peas.

Everything with love. Stay safe.

So we need to be careful exactly what is derived from original findings versus what is Chen's guess? I have hoped that everything in the summarising text was supported by original findings (maybe in his books or journal articles).

Bill, what is your alternative proposal of a theory of ancient Japanese style scoring rules but with group tax in China?

There are simpler shapes for life with two strings:

Click Here To Show Diagram Code

[go]$$B
$$ ------------------
$$ | . X X O . . . . .
$$ | X . X O . . . . .
$$ | O X X O . . . . .
$$ | O O O O . . . . .
$$ | . . . . . . . . .
$$ | . . . . . . . . .
$$ | . . . . . . . . .
$$ | . . . . . . . . .
$$ | . . . . . . . . .[/go]

Click Here To Show Diagram Code

[go]$$B
$$ ------------------
$$ | . . O O O O . . .
$$ | . O O X X O O . .
$$ | . O X . X X O . .
$$ | . O X X . X O . .
$$ | . O O X X O O . .
$$ | . . O O O O . . .
$$ | . . . . . . . . .
$$ | . . . . . . . . .
$$ | . . . . . . . . .[/go]

John: I've followed Robert's discussions of rules and strategy on L19, many of his contributions on Sensei's, and read some of his older RGG posts.

Ambiguity or lack of context seem to be the problem in this case, and neither one seems best addressed by a complaint about "proper English".

_________________
Occupy Babel!

Well, since even Robert is aware of the problem ("Common English might prefer "live group" instead of "alive group", I'd guess. When I say "alive group", I am im rules language mode..." - alive is a predicate adjective not an attributive), do you really want to derail a thread over such a petty topic?

John, it is a matter of what a particular piece of language emphasises. Ordinary texts emphasise conformity to common language. Some rules research texts emphasise precision in the form of strict usage of terms and no usage of non-term words that can be confused with terms.

hyperpape, I have presumed the context of basic go terms (like "independently alive").

Nothing is derived from the originals without guesswork. We do know that the scores are compatible with territory scoring with a group tax. We do have an example where the last dame does not affect the score. We do have an example where the text talks about each player having made the same number of moves, but White's last move does not appear in the diagram.

Click Here To Show Diagram Code

[go]$$ End position
$$ ---------------
$$ | . O X X . . . |
$$ | . O O X X . X |
$$ | . O O X X X X |
$$ | . O X , X O O |
$$ | O O X X X O . |
$$ | O X X O X O O |
$$ | X X O O O O . |
$$ ---------------[/go]

Here is a 7x7 position where White wins by 1 point by either area or territory scoring. Each player has played 19 stones. By stone scoring, however, Black wins by 1 point. Black has a group tax of 2 points, White has a group tax of 4 points.

What about the result under no pass go with prisoner return? That is actually a form of territory scoring. That is, when only territory remains, instead of playing the game out to the bitter end, the player may stop and score the game. (There is no jigo. If the net score is 0, the player to move loses.) White has 6 points of territory and Black has 5 points of territory. However, to get the correct score we must apply the group tax. Then White has 2 points and Black has 3. Black wins by 1 point.

What does that mean under no pass go with prisoner return? It means that Black wins (barely), even if Black plays first. (In this position playing first is a disadvantage.)

Click Here To Show Diagram Code

[go]$$B Continuation
$$ ---------------
$$ | . O X X 5 1 . |
$$ | 2 O O X X 3 X |
$$ | 4 O O X X X X |
$$ | . O X , X O O |
$$ | O O X X X O . |
$$ | O X X O X O O |
$$ | X X O O O O . |
$$ ---------------[/go]

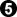
resigns. Under no pass go with prisoner return, after the score is 0 with White to play. Black wins.

Click Here To Show Diagram Code

[go]$$ Penultimate position
$$ ---------------
$$ | . O X X . . . |
$$ | . O O X X . X |
$$ | . O O X X X X |
$$ | . O X , X O O |
$$ | O O X X X O . |
$$ | O X X O X O O |
$$ | . X O O O O . |
$$ ---------------[/go]

Here is the position with 1 Black stone removed to leave a Japanese dame. Under stone scoring whoever gets the dame wins by 1 point. Under no pass go with prisoner return, aka territory scoring with a group tax, the position is worth 1*, where * is the dame. No matter who gets the dame, the score will be a 1 pt. win for Black.

Note that no pass go with prisoner return gives a good explanation for the group tax. The tax stands for moves the player cannot afford to make. (Each move is worth 1 point at the end.) It also explains why who gets the last dame does not affect the score. (It may affect who wins when the score is 0, however.)

Now, I am not claiming that no pass go with prisoner return was an older form of go, which led to territory scoring with a group tax. However, it does show that a group tax is compatible with territory scoring. If some form of no pass go was an ancestor, it would explain why go was played without a pass into the 20th century. Play did not end by passing, but by agreement (just as it would in a scorable position in no pass go). One of the questions that arose in the Segoe-Takahashi rules dispute was whether a player had a right to move or an obligation to do so.

_________________
The Adkins Principle:
At some point, doesn't thinking have to go on?
— Winona Adkins

Visualize whirled peas.

Everything with love. Stay safe.

In no pass go with prisoner return, when you run out of prisoners, do you pay a pass stone from your bowl?

I guess I need to think more carefully until I understand in general why no pass go with prisoner return gives a good explanation for the group tax and why a group tax is compatible with territory scoring. The topics are familiar but I never trust such statements until I see the proof:)

Assuming that you have no play on the board (except a disastrous one), you resign.



To understand the proof, you have to see that, after the dame stage, each play costs one point. That is when the players can stop and agree to the score. You also have to see that with prisoner return, playing inside your opponent's territory gains nothing except perhaps time. You also have to agree that sacrificing a live group after the dame stage gains nothing. (That may not be true in rare positions where you can reclaim the territory.)

In the example given, consider the play by no pass go with prisoner return in each territory instead of the whole board. You may verify that Black has three more moves that White in the Black territory, that White has two more moves than Black in the top left White territory, and that neither player has a move in the bottom right White territory.

_________________
The Adkins Principle:
At some point, doesn't thinking have to go on?
— Winona Adkins

Visualize whirled peas.

Everything with love. Stay safe.

I thought the original reference to proper English was a petty way of brushing aside one of Robert's questions, hence my reaction. I don't see a reason to think otherwise, but you're right that it derails the thread to disagree with something like that.

_________________
Occupy Babel!

Huh?
So 'a live group' and 'alive group' are two different things?
I guess it all depends on the spacing...

_________________
- Bantari
______________________________________________
WARNING: This post might contain Opinions!!

It depends on accepted presuppositions. E.g., in strict rules English, if I work with the Japanese 2003 Rules, then "alive" is defined and so may be used while "live" is undefined and may not be used. (One could define though: "Live is alive. Life is alive. Living is alive.")

E.g., in ordinary English, presuppositions are different. There all grammatical forms of a word (in a particular meaning - not in an entirely different meaning) are already assumed to have (about) the same meaning as one particular representative grammatical form.

Things become complicated when ordinary English is used in all its variation power with different meanings for the same word, see the World Amateur Go Championship Rules with their many very different meanings of "surrounded" etc.

Lawyers like nouns so much because they have an only restricted grammatical variation. Careful rules writers or mathematicians like defined terms so much because they (almost) do not have any variation.

John, just in case you should want to correct typos, I have found two: " ." can be "." and "is will be" can be "will be".

***

The text speaks of "simplify" in the context that territory counting would simplify stone scoring. This makes no sense to me. It would make sense as "decreases the number of plays made until counting". Is "simplify" Chen's word or has it been introduced in the English translation?

I am having difficulty with the contents where it concerns the last move of an equal number of moves. If the last move of an unequal number of moves is removed / undone / not made, then (usually) this does not affect Japanese counting of a game stopped before the territory filling encore because dame are worthless. Does this mean that the last move removal in case of an unequal move number is done only if (sort of) stone scoring is counted directly? Or is always the last move removed in case of an unequal move number - even if this removes just a dame - so that at least in principle (sort of) stone scoring counted directly would yield the same result? Does this even mean that Tang rules had a form of equivalence scoring? About 12 centuries earlier than its rediscovery in the 20th century? (IOW, people at that ancient time were pretty much as educated as people nowadays. Also the printing of texts is noteworthy; at German schools you learn nothing but Gutenberg's "invention"; a reinvention of course...)

Is it really stone scoring?! From the text, I would rather guess that it was Tang Scoring, i.e., stone scoring modified by not scoring the last move in case of an unequal move number. Do you agree? - I have learned to be cautious: Does it or does it not create pass fights? (If it does, then that side effect would have been overlooked by Tang people.) - Tang Scoring can have evolved from stone scoring or from area scoring ("complete" with allowed "overflow", i.e. filling of the eyes of two-eye-formations but no removal). So the history of pre-Tang (or very early Tang) scoring is not necessarily solved yet.

Another question is whether Tang had only territory counting or whether both options of stone counting or territory counting were used.

Robert

You are trying far too hard to make the very slender evidence bear more than it can. You have it all. Chen is not sitting on some secret pile of information. Admittedly you may find it hard to go through the extra details in his long articles and books, but essentially you have (or can have) what he has as regards the Tang to Yuan eras, because all the games and most of the texts (translated) are available on the GoGoD CD, and that includes the Ming book that elucidates the changeover in Chinese rules. There are probably hints as regards rules in go terms used in ancient Japan (Tale of Genji etc). A long discussion of that too is on the CD. There are possibly clues in the Go Shiki other than the ones I mentioned in the piece of Genji, but I haven't published those bits yet. I don't know whether Chen has looked at the old Japanese texts yet. If not, you have even more than he has.

I repeat, essentially you have access to what Chen has, and I think you need to examine all that before you try to wrestle with his latest text (written for the layman, recall). Even then, the amount of evidence is not going to grow, so there will be many uncertain areas.

You are likewise reading far, far, far, far too much into "simplify". (For the benefit of others, Chen simply said: "People tend to simplify habitually, so the last dame will be ignored" the relevant Chinese text was 人们总是习惯的趋向简化). He is just talking about human nature, not n-simplification and q-simplification.