Thermography
-
Gérard TAILLE
- Gosei
- Posts: 1346
- Joined: Sun Aug 23, 2020 2:47 am
- Rank: 1d
- GD Posts: 0
- Has thanked: 21 times
- Been thanked: 57 times
Re: Thermography
[quote="Bill Spight"]
It was known in the 1970s that there is a problem with the idea of double sente. See Ogawa-Davies, for instance. OC, there are global double sente, but they depend upon what else is on the board. In terms of CGT evaluation or even traditional evaluation of go positions, they do not exist. Circa 1980 I submitted an article to Go World to that effect, but it was not accepted. {shrug} For more on double sente, see https://senseis.xmp.net/?DoubleSenteIsRelative .
[quote]
I am a little surprise to read that double sente do not exist.
As soon as you propose a defintion for a double sente it exists doesn't it ?
Inherently, I agree that defining a sente or double sente move maybe a difficulty but in the context of an environment with a temperature t it seems quite obvious:
If black plays a move and the threat after this move is greater or egal to t then the black move is sente.
If at the same time a white play creates a threat also greater or equal to t then it is a double sente.
It was known in the 1970s that there is a problem with the idea of double sente. See Ogawa-Davies, for instance. OC, there are global double sente, but they depend upon what else is on the board. In terms of CGT evaluation or even traditional evaluation of go positions, they do not exist. Circa 1980 I submitted an article to Go World to that effect, but it was not accepted. {shrug} For more on double sente, see https://senseis.xmp.net/?DoubleSenteIsRelative .
[quote]
I am a little surprise to read that double sente do not exist.
As soon as you propose a defintion for a double sente it exists doesn't it ?
Inherently, I agree that defining a sente or double sente move maybe a difficulty but in the context of an environment with a temperature t it seems quite obvious:
If black plays a move and the threat after this move is greater or egal to t then the black move is sente.
If at the same time a white play creates a threat also greater or equal to t then it is a double sente.
-
Bill Spight
- Honinbo
- Posts: 10905
- Joined: Wed Apr 21, 2010 1:24 pm
- Has thanked: 3651 times
- Been thanked: 3373 times
Re: Thermography
Not necessarily.Gérard TAILLE wrote:I am a little surprise to read that double sente do not exist.Bill Spight wrote: It was known in the 1970s that there is a problem with the idea of double sente. See Ogawa-Davies, for instance. OC, there are global double sente, but they depend upon what else is on the board. In terms of CGT evaluation or even traditional evaluation of go positions, they do not exist. Circa 1980 I submitted an article to Go World to that effect, but it was not accepted. {shrug} For more on double sente, see https://senseis.xmp.net/?DoubleSenteIsRelative .
As soon as you propose a defintion for a double sente it exists doesn't it ?
What you are describing is a global double sente, which do exist. However, for a large enough ambient temperature a play in such a position by one player or another will not be global sente. Global double sente are relative to what else is on the board. There is no such think as an intrinsic, locally defined double sente, except those in which the sente plays do not gain anything. Seki, for example.Inherently, I agree that defining a sente or double sente move maybe a difficulty but in the context of an environment with a temperature t it seems quite obvious:
If black plays a move and the threat after this move is greater or egal to t then the black move is sente.
If at the same time a white play creates a threat also greater or equal to t then it is a double sente.
The Adkins Principle:
At some point, doesn't thinking have to go on?
— Winona Adkins
Visualize whirled peas.
Everything with love. Stay safe.
At some point, doesn't thinking have to go on?
— Winona Adkins
Visualize whirled peas.
Everything with love. Stay safe.
-
Bill Spight
- Honinbo
- Posts: 10905
- Joined: Wed Apr 21, 2010 1:24 pm
- Has thanked: 3651 times
- Been thanked: 3373 times
Re: Thermography
So the choice for Black comes down to the kosumi or the large monkey jump.  Now, we already know that these two are incomparable, but let's take a look with difference games.
Now, we already know that these two are incomparable, but let's take a look with difference games.
There are different ways of replying to the monkey jump. Let's look at a few.
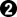 is the usual reply, but here it looks passive.
is the usual reply, but here it looks passive.
White goes first on both boards and plainly wins. Can Black do better?
 fills ko.
fills ko.
White wins again. Obviously. Now let Black play first.
White wins again.
 fills ko.
fills ko.
White wins yet again.
If Black is going to reply like this, plainly the monkey jump is better.
Let's look at a different reply to the monkey jump.
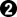 is the usual reply, but here it looks passive. OTOH, Black has
is the usual reply, but here it looks passive. OTOH, Black has 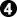 , which I overlooked the other day.
, which I overlooked the other day. 
 connects.
connects.
Black has nothing better. White wins by 2 points.
 captures two White stones to win by 1 point. White has nothing better. Black's play does not depend on winning a ko fight.
captures two White stones to win by 1 point. White has nothing better. Black's play does not depend on winning a ko fight.
So with the replies at 2 and 4, the plays are incomparable.
What about the reply that I found the other day? How does it compare with 2 and 4?
1 prisoner
prisoner
To win, avoids a mirror image. Still,
avoids a mirror image. Still,  manages to make jigo. All roads lead to Rome.
manages to make jigo. All roads lead to Rome.
White's reply on the left, sacrificing a stone, is at least as good as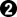 and
and 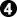 on the right.
on the right.
1 prisoner
prisoner
White plays to avoid a mirror image.
to avoid a mirror image.  fills the ko to win by 1 pt.
fills the ko to win by 1 pt.
1 prisoner
prisoner
 protects on the right, but White captures two stones on the left to win by 1 pt.
protects on the right, but White captures two stones on the left to win by 1 pt.
So my feeling was correct. The sacrifice is the correct reply to the monkey jump.

In case it's not obvious, let's put the icing on the cake. There is another reply.
There is another reply.
1 prisoner
prisoner
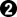 is a sacrifice you see from time to time, but it doesn't look too good here, eh?
is a sacrifice you see from time to time, but it doesn't look too good here, eh?
1 prisoner, 1
prisoner, 1  prisoner
prisoner
 takes back
takes back
White wins by 2 pts. Black has nothing better.
1 prisoner, 1
prisoner, 1  prisoner
prisoner
Black saves his two stones, but White saves his to get jigo.
1 prisoner, 1
prisoner, 1  prisoner
prisoner
 connects, for jigo this way.
connects, for jigo this way.
So my sacrifice is the right one.
Hmmm. Is there no other good reply?
1 prisoner
prisoner
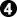 threatens to throw in at 5 and capture
threatens to throw in at 5 and capture  . But then
. But then  threatens to kill.
threatens to kill.
The right side is settled. Either player wins by playing on the left. So these plays are incomparable.
I took my bows too soon.
There are different ways of replying to the monkey jump. Let's look at a few.
White goes first on both boards and plainly wins. Can Black do better?
White wins again. Obviously. Now let Black play first.
White wins again.
White wins yet again.
If Black is going to reply like this, plainly the monkey jump is better.
Let's look at a different reply to the monkey jump.
Black has nothing better. White wins by 2 points.
So with the replies at 2 and 4, the plays are incomparable.
What about the reply that I found the other day? How does it compare with 2 and 4?
1
To win,
White's reply on the left, sacrificing a stone, is at least as good as
1
White plays
1
So my feeling was correct. The sacrifice is the correct reply to the monkey jump.
In case it's not obvious, let's put the icing on the cake.
1
1
White wins by 2 pts. Black has nothing better.
1
Black saves his two stones, but White saves his to get jigo.
1
So my sacrifice is the right one.
Hmmm. Is there no other good reply?
1
The right side is settled. Either player wins by playing on the left. So these plays are incomparable.
I took my bows too soon.
The Adkins Principle:
At some point, doesn't thinking have to go on?
— Winona Adkins
Visualize whirled peas.
Everything with love. Stay safe.
At some point, doesn't thinking have to go on?
— Winona Adkins
Visualize whirled peas.
Everything with love. Stay safe.
-
Bill Spight
- Honinbo
- Posts: 10905
- Joined: Wed Apr 21, 2010 1:24 pm
- Has thanked: 3651 times
- Been thanked: 3373 times
Re: Thermography
Just to check. 
1 prisoner
prisoner
1 prisoner
prisoner
White wins. Black has nothing better.
1 prisoner
prisoner
Black wins.
1 prisoner
prisoner
 fills the ko and wins.
fills the ko and wins.
So these plays are incomparable.
One more time.
 captures one stone and wins.
captures one stone and wins.
 connects, but
connects, but 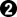 makes jigo.
makes jigo.
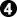 fills the ko, for jigo.
fills the ko, for jigo.
So we can discard Reply 3, and Monkey Jump 1 is incomparable with the sacrifice.
Just one more time.
Suppose Black extends on the edge instead of jumping. It looks nuts, but let's see.
 connects
connects
White wins. Black has nothing better.
Black wins.
The two plays are incomparable.
Well, I guess we have to check it with the sacrifice.
1 prisoner
prisoner
Black connects, White makes jigo.
1 prisoner
prisoner
 connects to win. White has nothing better.
connects to win. White has nothing better.
1 prisoner
prisoner
Jigo.
1 prisoner
prisoner
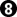 connects, for jigo.
connects, for jigo.
1 prisoner
prisoner
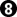 connects, for jigo.
connects, for jigo.
This may eliminate the extension.
1
1
White wins. Black has nothing better.
1
Black wins.
1
So these plays are incomparable.
One more time.
So we can discard Reply 3, and Monkey Jump 1 is incomparable with the sacrifice.
Just one more time.
Suppose Black extends on the edge instead of jumping. It looks nuts, but let's see.
White wins. Black has nothing better.
Black wins.
The two plays are incomparable.
Well, I guess we have to check it with the sacrifice.
1
Black connects, White makes jigo.
1
1
Jigo.
1
1
This may eliminate the extension.
The Adkins Principle:
At some point, doesn't thinking have to go on?
— Winona Adkins
Visualize whirled peas.
Everything with love. Stay safe.
At some point, doesn't thinking have to go on?
— Winona Adkins
Visualize whirled peas.
Everything with love. Stay safe.
-
Gérard TAILLE
- Gosei
- Posts: 1346
- Joined: Sun Aug 23, 2020 2:47 am
- Rank: 1d
- GD Posts: 0
- Has thanked: 21 times
- Been thanked: 57 times
Re: Thermography
For the time being I am still not convinced that kosumi is incomparable with the monkey jump.
Depending of the environment white must choose the correct answer between "a" or "b" and black must choose the correct answer between "c" or "d".
My reasonning is the following:
1) if the environment is such that a move at "c" is best in the right diagram then, in the left diagram, I decide with white to play "a" and black cannot win
2) if now the environment is such that a move at "d" is best in the right diagram then, in the left diagram, I decide with white to play "b" and here again black cannot win.
My conclusion is that it does not exist an environment in which the kosumi is better that the monkey jump. Where am I wrong?
Depending of the environment white must choose the correct answer between "a" or "b" and black must choose the correct answer between "c" or "d".
My reasonning is the following:
1) if the environment is such that a move at "c" is best in the right diagram then, in the left diagram, I decide with white to play "a" and black cannot win
2) if now the environment is such that a move at "d" is best in the right diagram then, in the left diagram, I decide with white to play "b" and here again black cannot win.
My conclusion is that it does not exist an environment in which the kosumi is better that the monkey jump. Where am I wrong?
-
Bill Spight
- Honinbo
- Posts: 10905
- Joined: Wed Apr 21, 2010 1:24 pm
- Has thanked: 3651 times
- Been thanked: 3373 times
Re: Thermography
Well, I got carried away with the difference games, eh? 
Constructing the thermograph
Truth to say, difference games are not necessary to thermography at all, and are hardly ever used. However, it was easy to show that the keima sente and the crawl sente are unnecessary. The kosumi sente dominates them. As I said, if they were gote, that would be a different matter. But anyway, all we have to consider are the kosumi sente and the large monkey jump sente. Let's review the reverse sente first.
 blocks on the second line. Play can, and usually does, stop there. If Black replies she plays the hane-and-connect for a local score of -5 in the marked region. Each player has made the same number of plays, so the Right wall of the thermograph rises as a vertical line at that point.
blocks on the second line. Play can, and usually does, stop there. If Black replies she plays the hane-and-connect for a local score of -5 in the marked region. Each player has made the same number of plays, so the Right wall of the thermograph rises as a vertical line at that point.
Black does not reply above temperature 1, so the wall turns 45° to the left at that temperature rising one degree for each point of territory. Remember, the leftward movement is positive, the reverse the usual convention. The equation of that line is v = -6 + t, where v is the territory and t is the temperature.
Now let's look at the kosumi sente.
The sente actually ends with but we consider what happens when Black keeps playing. The score after
but we consider what happens when Black keeps playing. The score after  is -2. Black has made one more move than White, so the line from here angles up and to the right. It's equation is v = -2 - t. How far up does it go?
is -2. Black has made one more move than White, so the line from here angles up and to the right. It's equation is v = -2 - t. How far up does it go?
If I didn't already know, it would be easy to work out that this is correct play at temperature 1. White could get an equivalent result, except for ko threats, by starting at 2. Each player has made the same number of plays, including the kosumi sente exchange, so the line rises vertically at -3. These two lines intersect at v = -3, t = 1. Above temperature 1 the prospective wall, called a scaffold, rises vertically at -3, below temperature 1 it angles down to -2 at temperature 0.
Now let's look at the monkey jump.
This is one of the main lines, with the throw-in, . White could also get here by starting at 4. That's the other main line. The usual reply is at 6. We'll consider that later.
. White could also get here by starting at 4. That's the other main line. The usual reply is at 6. We'll consider that later.
What if Black continues?
1 prisoner
prisoner
 connects the Black stones,
connects the Black stones,  makes a second eye, and
makes a second eye, and  saves the four stones. The local score is 0. Since Black has made one more move than White, the scaffold angles up from 0 to the right at one point of territory for each degree of temperature. The equation of the line is v = -t.
saves the four stones. The local score is 0. Since Black has made one more move than White, the scaffold angles up from 0 to the right at one point of territory for each degree of temperature. The equation of the line is v = -t.
How high does it go? To find out, let's look at the White follow-up after the sente.
1 prisoner
prisoner
There is a ko, which White can take and win on the usual assumption of no ko threats. But comes to the same thing.
comes to the same thing.  After
After  the local score is -4. Since White has made one more move than Black, the scaffold angles up from there to the left. It's equation is v = -4 + t. Note that this is the scaffold for the position after the sente, not the scaffold for the original position. The scaffolds intersect at t = 2, v = -2. The mast rises vertically from there. The scaffold for this sente is v = -2 above temperature 2 and v = -4 + t below temperature 2.
the local score is -4. Since White has made one more move than Black, the scaffold angles up from there to the left. It's equation is v = -4 + t. Note that this is the scaffold for the position after the sente, not the scaffold for the original position. The scaffolds intersect at t = 2, v = -2. The mast rises vertically from there. The scaffold for this sente is v = -2 above temperature 2 and v = -4 + t below temperature 2.
There is another variation to consider.
 does not play the throw-in, but it threatens it.
does not play the throw-in, but it threatens it.  prevents that, with sente. As we have seen, with a different order of play, this line is incomparable with the throw-in. After
prevents that, with sente. As we have seen, with a different order of play, this line is incomparable with the throw-in. After  the local score is -1. The scaffold rises vertically from there. OC, that is worse for White than -2, so this line is not as good as the throw-in above temperature 2. But it is better for White than 0, so we find the intersection v = -t and v = -1 to find where White switches to this line of play. The intersection is at t = 1, v = -1. So for the reply of
the local score is -1. The scaffold rises vertically from there. OC, that is worse for White than -2, so this line is not as good as the throw-in above temperature 2. But it is better for White than 0, so we find the intersection v = -t and v = -1 to find where White switches to this line of play. The intersection is at t = 1, v = -1. So for the reply of  the scaffold is vertical at -2 above temperature 2, angling down below temperature 2 to -1 at temperature 1, and vertical below that to -1 at temperature 0.
the scaffold is vertical at -2 above temperature 2, angling down below temperature 2 to -1 at temperature 1, and vertical below that to -1 at temperature 0. 
BTW, what if Black does not connect with in the previous diagram, but tries to kill?
in the previous diagram, but tries to kill?
Now White cannot play at a because of damezumari. Oh, for a dame!
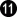 at 8
at 8
White has no external threats, by assumption, but the play has generated a local threat for White at . With a dame White would not have needed to play the ko.
. With a dame White would not have needed to play the ko. 
More later.
Constructing the thermograph
Truth to say, difference games are not necessary to thermography at all, and are hardly ever used. However, it was easy to show that the keima sente and the crawl sente are unnecessary. The kosumi sente dominates them. As I said, if they were gote, that would be a different matter. But anyway, all we have to consider are the kosumi sente and the large monkey jump sente. Let's review the reverse sente first.
Black does not reply above temperature 1, so the wall turns 45° to the left at that temperature rising one degree for each point of territory. Remember, the leftward movement is positive, the reverse the usual convention. The equation of that line is v = -6 + t, where v is the territory and t is the temperature.
Now let's look at the kosumi sente.
The sente actually ends with
If I didn't already know, it would be easy to work out that this is correct play at temperature 1. White could get an equivalent result, except for ko threats, by starting at 2. Each player has made the same number of plays, including the kosumi sente exchange, so the line rises vertically at -3. These two lines intersect at v = -3, t = 1. Above temperature 1 the prospective wall, called a scaffold, rises vertically at -3, below temperature 1 it angles down to -2 at temperature 0.
Now let's look at the monkey jump.
This is one of the main lines, with the throw-in,
What if Black continues?
1
How high does it go? To find out, let's look at the White follow-up after the sente.
1
There is a ko, which White can take and win on the usual assumption of no ko threats. But
There is another variation to consider.
BTW, what if Black does not connect with
Now White cannot play at a because of damezumari. Oh, for a dame!
White has no external threats, by assumption, but the play has generated a local threat for White at
More later.
The Adkins Principle:
At some point, doesn't thinking have to go on?
— Winona Adkins
Visualize whirled peas.
Everything with love. Stay safe.
At some point, doesn't thinking have to go on?
— Winona Adkins
Visualize whirled peas.
Everything with love. Stay safe.
-
Bill Spight
- Honinbo
- Posts: 10905
- Joined: Wed Apr 21, 2010 1:24 pm
- Has thanked: 3651 times
- Been thanked: 3373 times
Re: Thermography
OK, I guess I made some assumptions that may not hold. Fair enough.Gérard TAILLE wrote: For the time being I am still not convinced that kosumi is incomparable with the monkey jump.
I suppose that you will grant that there are environments in which the large monkey jump is better. If there is an environment in which the kosumi is better, then the kosumi and the monkey jump are incomparable. (Assuming that both are sente, threatening to kill, OC.)My conclusion is that it does not exist an environment in which the kosumi is better that the monkey jump.
Let's start at the very beginning.
This mirror position has a value of 0. Whoever plays first, the second player can play mirror go for jigo. (Note: The relevant positions do not have to be on different boards. The point is that they are independent of each other.)
Let Black play first and play the kosumi, and let White reply with the large monkey jump.
Can Black to play win the difference game from this point? If so, then there is an environment where the kosumi is better than the monkey jump. Namely, the one after
Obviously, if
1
Now if White connects at 13, Black will atari on the right to transpose to the previous variation and win the difference game. So White saves his stones on the right and Black continues on the left. In the end Black wins by 1 pt.
The Adkins Principle:
At some point, doesn't thinking have to go on?
— Winona Adkins
Visualize whirled peas.
Everything with love. Stay safe.
At some point, doesn't thinking have to go on?
— Winona Adkins
Visualize whirled peas.
Everything with love. Stay safe.
-
Gérard TAILLE
- Gosei
- Posts: 1346
- Joined: Sun Aug 23, 2020 2:47 am
- Rank: 1d
- GD Posts: 0
- Has thanked: 21 times
- Been thanked: 57 times
Re: Thermography
OK Bill, let's consider an environment for which, afterBill Spight wrote: Let's start at the very beginning.
This mirror position has a value of 0. Whoever plays first, the second player can play mirror go for jigo. (Note: The relevant positions do not have to be on different boards. The point is that they are independent of each other.)
Let Black play first and play the kosumi, and let White reply with the large monkey jump.
Can Black to play win the difference game from this point? If so, then there is an environment where the kosumi is better than the monkey jump. Namely, the one after, because White can make jigo by playing the kosumi.
captures two stones
Obviously, ifkills on the left,
will kill on the right, for jigo.
must come back to save the White group on the left. Black wins by 1 pt.
1prisoner,
connects
is clever play.

If
plays the atari on the right side board,
will play atari with sente on the left and win. For Black the atari at 13 is tempting, but White will atari and make a mirror position, for jigo. So, faute de mieux,
plays the solid connection.
Now if White connects at 13, Black will atari on the right to transpose to the previous variation and win the difference game. So White saves his stones on the right and Black continues on the left. In the end Black wins by 1 pt.
I agree in this case that the move
In other words: Well you found an environment for which the move "a" is better than the move "c" but, for this environment, the move "b" is still better than the move "a". Where is the gain Bill?
-
Bill Spight
- Honinbo
- Posts: 10905
- Joined: Wed Apr 21, 2010 1:24 pm
- Has thanked: 3651 times
- Been thanked: 3373 times
Re: Thermography
In this situation, the kosumi at a is better than the keima at b.Gérard TAILLE wrote: Well you found an environment for which the move "a" is better than the move "c" but, for this environment, the move "b" is still better than the move "a". Where is the gain Bill?
Black first can win, White first cannot. Therefore the kosumi dominates the keima.
The only time that the keima may be better depends on a possible ko.
Edit: The point being that difference games depend on the different positions being independent, and kos can break independence.
The Adkins Principle:
At some point, doesn't thinking have to go on?
— Winona Adkins
Visualize whirled peas.
Everything with love. Stay safe.
At some point, doesn't thinking have to go on?
— Winona Adkins
Visualize whirled peas.
Everything with love. Stay safe.
-
Gérard TAILLE
- Gosei
- Posts: 1346
- Joined: Sun Aug 23, 2020 2:47 am
- Rank: 1d
- GD Posts: 0
- Has thanked: 21 times
- Been thanked: 57 times
Re: Thermography
Surely the kosumi can be better than the keima depending of the environment but this is not my point which is the following:Bill Spight wrote:In this situation, the kosumi at a is better than the keima at b.Gérard TAILLE wrote: Well you found an environment for which the move "a" is better than the move "c" but, for this environment, the move "b" is still better than the move "a". Where is the gain Bill?
plays at a to win.
makes jigo.
Black first can win, White first cannot. Therefore the kosumi dominates the keima.
The only time that the keima may be better depends on a possible ko.
Edit: The point being that difference games depend on the different positions being independent, and kos can break independence.
Because kosumi and monkey jump are incomparable it exists a set of environment E for which the kosumi is strictly better than the monkey jump and now is my point : whatever environment you choose in E the small keima is equivalent or better than the kosumi !
Of course I am not sure at 100% but it is my point.
If this is true we will conclude that the kosumi possibility can be simply ignored.
BTW if it happens that, for each environment in E, the kosumi and the small keima are equivalent then you can also ignore the keima and keep the kosumi. I have to study this point but this is another issue.
-
Bill Spight
- Honinbo
- Posts: 10905
- Joined: Wed Apr 21, 2010 1:24 pm
- Has thanked: 3651 times
- Been thanked: 3373 times
Re: Thermography
I may have been a bit unclear about the environment. It is the rest of the board from the position in question.Gérard TAILLE wrote:Surely the kosumi can be better than the keima depending of the environmentBill Spight wrote:In this situation, the kosumi at a is better than the keima at b.Gérard TAILLE wrote: Well you found an environment for which the move "a" is better than the move "c" but, for this environment, the move "b" is still better than the move "a". Where is the gain Bill?
plays at a to win.
makes jigo.
Black first can win, White first cannot. Therefore the kosumi dominates the keima.
The only time that the keima may be better depends on a possible ko.
Edit: The point being that difference games depend on the different positions being independent, and kos can break independence.
For example:
I have marked the empty points in the environment. They are outside the problem area and independent of it. In this case they are Black territory, but that is of zero consequence to the questions being asked.
For the difference game:
The environment for the difference game is the sum of the environment on one board plus its mirror opposite. As long as the environment on the original board is not implicated in a ko fight, it does not matter what it is. The sum of it and its opposite is zero.
For example:
In this case the environment on the left contains an unsettled group, but the environment on the right contains its opposite. If either player plays in the environment on one side, the other player can mirror that move on the other side and maintain an environment of zero. (You see how ko fights can mess up the logic of difference games.
The position on the left side as the environment of the position on the right
Let
White could make jigo by playing the kosumi on the right side. However, if White plays elsewhere on the right side and Black is able then to win the difference game with correct play, then there exists an environment such that the kosumi is better than that other play.
We don't have to find such an environment. The existence of one is part of the logic of difference games.
More later.
Edit: OK, here is a little more.
If there exists a (non-ko fight) environment such that play A is better than play B, and there also exists such an environment such that play B is better than play A, then play A and play B are incomparable. We cannot say that one is better than the other.
However, if there exists such an environment that play A is better than play B, but not the other way around, then play A dominates play B (with the caveat about ko fights or potential ko fights).
Here the kosumi and the large monkey jump are incomparable, but the kosumi dominates both the crawl and the keima (small monkey jump).
The Adkins Principle:
At some point, doesn't thinking have to go on?
— Winona Adkins
Visualize whirled peas.
Everything with love. Stay safe.
At some point, doesn't thinking have to go on?
— Winona Adkins
Visualize whirled peas.
Everything with love. Stay safe.
-
Gérard TAILLE
- Gosei
- Posts: 1346
- Joined: Sun Aug 23, 2020 2:47 am
- Rank: 1d
- GD Posts: 0
- Has thanked: 21 times
- Been thanked: 57 times
Re: Thermography
With your last post I believe I have found where is the misunderstanding.
The point is quite subtil: considering the environment we both exclude pure ko threats like for example: But you seem also to exclude from the environment "normal" sente move like for example:
Because in my mind I accept such environment which allows to use a sente move as a ko threat our conclusions are logically different
Here is an example for the dicussion kosumi vs keima
You can see that after a white move at "a", white may create a sente move at "b" which can be use as a ko threat. That is the point.
As you see, it is not so easy to define what a non-ko fight environment is and, in addition, the restriction to such non-ko fight environment seems really very severe doesn't it?
Anyway Bill, an interesting discussion !
The point is quite subtil: considering the environment we both exclude pure ko threats like for example: But you seem also to exclude from the environment "normal" sente move like for example:
Because in my mind I accept such environment which allows to use a sente move as a ko threat our conclusions are logically different
Here is an example for the dicussion kosumi vs keima
You can see that after a white move at "a", white may create a sente move at "b" which can be use as a ko threat. That is the point.
As you see, it is not so easy to define what a non-ko fight environment is and, in addition, the restriction to such non-ko fight environment seems really very severe doesn't it?
Anyway Bill, an interesting discussion !
-
Bill Spight
- Honinbo
- Posts: 10905
- Joined: Wed Apr 21, 2010 1:24 pm
- Has thanked: 3651 times
- Been thanked: 3373 times
Re: Thermography
Yes and no. In theory, it's quite a severe restriction, although I'm afraid I gave you the wrong impression of the problem, but in practice it is not such a problem.Gérard TAILLE wrote:As you see, it is not so easy to define what a non-ko fight environment is and, in addition, the restriction to such non-ko fight environment seems really very severe doesn't it?
Should White play at a or b?
A difference game will find that they are equivalent. But of course White should play at a, because if White plays at b, Black might reply at a and leave a ko threat behind. There may or may not be a ko or potential ko in the environment, and if there is, this ko threat may not matter, but nothing is lost by avoiding it.
Or consider these sequences.
White may play this way in certain situations so as not to leave any local play behind. However,
Because of damezumari, Black can play
However, that would be exceptional, and a caveat to that effect allows us to draw valuable conclusions from difference games for this position. Conway and Berlekamp, who developed difference games, avoided kos in difference games because you can't prove anything in that case. I, however, do not mind defeasible reasoning with exceptions, as long as you mention the caveats. Conway and Berlekamp only applied difference games to non-ko positions, with the general warning that the conclusions only applied to non-ko environments. That was something they had proved. Usually the conclusions also apply to environments with kos or potential kos, as those possibilities are normally irrelevant to any specific comparison.
The Adkins Principle:
At some point, doesn't thinking have to go on?
— Winona Adkins
Visualize whirled peas.
Everything with love. Stay safe.
At some point, doesn't thinking have to go on?
— Winona Adkins
Visualize whirled peas.
Everything with love. Stay safe.
-
Gérard TAILLE
- Gosei
- Posts: 1346
- Joined: Sun Aug 23, 2020 2:47 am
- Rank: 1d
- GD Posts: 0
- Has thanked: 21 times
- Been thanked: 57 times
Re: Thermography
OK, Bill let me try a difference game:
If I would try to prove that kosumi does not dominate the keima I have to find a way to win the above diference game with white, right?
I see clearly that I cannot win by beginning at "b" => no choice for my first white move:
Now it is black turn. If black plays at "a" white plays at "b" and win => black must ansmer at "a" and the following sequence seems mandatory
then white can simply continue by winning the game.
Isn't it correct?
If I would try to prove that kosumi does not dominate the keima I have to find a way to win the above diference game with white, right?
I see clearly that I cannot win by beginning at "b" => no choice for my first white move:
Now it is black turn. If black plays at "a" white plays at "b" and win => black must ansmer at "a" and the following sequence seems mandatory
then white can simply continue by winning the game.
Isn't it correct?
-
Gérard TAILLE
- Gosei
- Posts: 1346
- Joined: Sun Aug 23, 2020 2:47 am
- Rank: 1d
- GD Posts: 0
- Has thanked: 21 times
- Been thanked: 57 times
Re: Thermography
Seeing the difference game in my previous post I built the following very simple position and very simple environment (without ko threat)
The keima seems better than the kosumi, doesn't it?
The keima seems better than the kosumi, doesn't it?