Gérard TAILLE wrote:Bill Spight wrote:
Well, double sente has been controversial for at least 45 years.
Oops I am not aware of these 45 years of controversial discussion.
Kano's
Yose Jiten came out in 1974. Kano defines double sente as a place where whoever plays first, Black or White, can play with sente. In the discussion of his very first example, he recognizes that one player may be much more likely to not reply than the other. Instead of admitting that in that case the position is really a sente for the other player, he introduces a new term,
hitsuzensei, meaning certainty or necessity. See previous discussion here:
https://www.lifein19x19.com/viewtopic.p ... 67#p178067
The Endgame by Ogawa and Davies came out in 1976. Davies' observation about dividing the so-called double sente value by 0 tolled the mathematical death-knell for double sente, but few go pros are mathematicians.
Maybe there is some misunderstandig on this point. Taking a real game with several subgames, my view is that subgames like the one I called "double blabla" may add some uncertainty on the result of the game. Because of that calculating acurate values for gote subgames might look irrelevant. To avoid that I would have liked to extract such positions from the set of gote but I see you do not like the idea. Considering all these positions as gote I fear that it will be more difficult for the theory to give reliable results.
Remember that a gote
position may be played
with sente, given the global situation. Which number is more likely to get the average non-mathematical player's attention, a "2 point double sente" or a "20 point gote"?

Let's concentrate essentially on gote.
Can you make the same exercice and define without any ambiguity what is gote, sente or maybe unknown position as I did.
Here is a prototypical gote thermograph. (BTW, humans reason pretty well with prototypes.

)
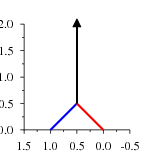
- gote 1-2.png (2.37 KiB) Viewed 16719 times
The left and right walls are each inclined, which indicates a play or sequence of plays made
with gote for each player playing first. Where they meet the black mast rises vertically, indicating that neither player will play in that game above that temperature (tax). This is how a gote thermograph looks where the left and right walls meet, whatever it may look like below that temperature.
Some thermographs for kos look similar, but the angles of the walls are different. As you know, ko thermographs can look strange.

Here is a prototypical sente thermograph.
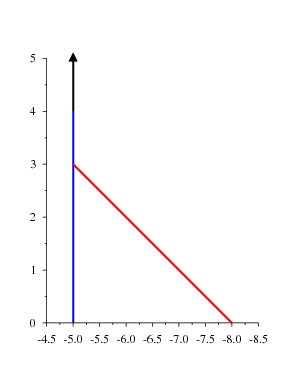
- sente 3 pt.png (4.07 KiB) Viewed 16719 times
The left wall of the thermograph is vertical, which indicates a sequence of plays with an even number of plays by each player, starting in this case with a Black play and ending with a White play. I.e., Black played
with sente. The right wall is inclined, indicating that White played with gote. Above where the walls meet the left wall rises vertically as the mast before the mast becomes black. The blue mast indicates the
privilege of Black to play first with sente in that temperature range. This is how a Black sente thermograph looks where the walls meet, no matter how it looks below that temperature. A White sente thermograph, OC, has a vertical right wall and an inclined left wall.
The thermograph of a gote has a black mast, below which each wall is inclined.
The thermograph of a sente has a blue or red mast where the walls meet, depending upon whose sente it is, below which the wall of that color descends vertically while the other wall is inclined.
There are non-ko positions that are ambiguous between sente and gote, with different thermographs. We have already seen one where the mast is blue where the walls meet, but the blue wall is inclined below that while the red wall is vertical!
