This 'n' that

Gérard TAILLE · **#901**

Click Here To Show Diagram Code: [go]$$B $$ --------------------- $$ | . . . . X X O O . | $$ | . . O O X X O O O | $$ | . . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O a . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

Click Here To Show Diagram Code: [go]$$B $$ --------------------- $$ | . 2 . b X X O O . | $$ | a 1 O O X X O O O | $$ | 3 . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O a . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

BTW, if you do not know the white move at "a" and you play white "b" then black is komaster and is able to kill the top left white corner.
Otherwise if white plays "a" he will be able to save his group by playing first at "a" and black has no more ko threat. But note that by playing at "a" white do not play in the environment in order to gain t points and that means that the black ko threat allows black to add t + 1 to her score (t for a play in the enviroment and +1 for the white move in white territory).
I do not know what is the correct wording here. Certainly black in not "komaster" but her ko threat cannot be ignore and will assure some good points.

Bill Spight · **#902**

Gérard TAILLE wrote:

Bill Spight wrote:

Oh, yes. Generally speaking the point of Black starting on the 2-2 is to make the ko, not to generate ko threats.

Up until now we have focused on the play that you discovered where Black makes the ko, despite neither player having a ko threat, now or later.

Evaluation of kos, except for placid kos, depends upon what assumptions we make. Berlekamp's brilliant komaster analysis depends upon assumptions that are usually not met exactly on the go board, but which provide useful approximate limits. When neither side is komaster, he came up with the idea of a neutral threat environment (NTE), where each player has the exact opposite of the ko threats of the other, where the ko threats are sufficiently large. How good an approximation NTE produces in practice is another question, but let's give it a shot.

Click Here To Show Diagram Code: [go]$$W White first $$ --------------------- $$ | C 5 4 2 X . . . . | $$ | 1 C O O X . . . . | $$ | C C O X X . . . . | $$ | C O O X . . . . . | $$ | . O X X . . . . . | $$ | 3 X . . . . . . . | $$ | . X . . . . . . . | $$ | X X . . . . . . . | $$ | . . . . . . . . . | $$ ---------------------[/go]

gets a local score of -5 in one net play.

Click Here To Show Diagram Code: [go]$$B Black first, no ko $$ --------------------- $$ | . 4 3 1 X . . . . | $$ | . 2 O O X . . . . | $$ | . . O X X . . . . | $$ | 6 O O X . . . . . | $$ | 5 O X X . . . . . | $$ | 7 X . . . . . . . | $$ | . X . . . . . . . | $$ | X X . . . . . . . | $$ | . . . . . . . . . | $$ ---------------------[/go]

gets a net local score of -3 in one net play.

Click Here To Show Diagram Code: [go]$$B Black first, ko, NTE $$ --------------------- $$ | 7 2 . 4 X . . . . | $$ | . 1 O O X . . . . | $$ | 3 . O X X . . . . | $$ | 6 O O X . . . . . | $$ | 5 O X X . . . . . | $$ | . X . . . . . . . | $$ | . X . . . . . . . | $$ | X X . . . . . . . | $$ | . . . . . . . . . | $$ ---------------------[/go]

Now we have reached a position after one net move by Black such that either player, playing first could win the ko in two local plays by ignoring the opponent's threat.

Click Here To Show Diagram Code: [go]$$W White first, NTE $$ --------------------- $$ | X O . O X . . . . | $$ | 1 X O O X . . . . | $$ | X 3 O X X . . . . | $$ | O O O X . . . . . | $$ | X O X X . . . . . | $$ | . X . . . . . . . | $$ | . X . . . . . . . | $$ | X X . . . . . . . | $$ | . . . . . . . . . | $$ ---------------------[/go]

= ko threat, :b4:

completes threat

After :b4:

there is a local score of -7 plus a gote worth on average 0 when t > 1.

Click Here To Show Diagram Code: [go]$$B Black first, NTE $$ --------------------- $$ | X W 1 W X . . . . | $$ | C X W W X . . . . | $$ | X 3 W X X . . . . | $$ | W W W X . . . . . | $$ | X W X X . . . . . | $$ | C X . . . . . . . | $$ | C X . . . . . . . | $$ | X X . . . . . . . | $$ | . . . . . . . . . | $$ ---------------------[/go]

= ko threat, :w4:

completes threat

After :w4:

there is a local score of +21.

By assumption, what each player gains by playing and completing their threat is the same, and therefore cancel out in the average, so the average value of the given position under NTE when t > 1 is the average of the value of these two politions. That value is (21 - 7)/2 = 7, 10 points better than -3.

So, under NTE conditions, the average value of the corner is (7 - 5)/2 = 1, and the miai value of a play is 6.

Though I follow your calculation the conclusion does not fit with my understanding of the miai value basic concept. For me a miai value of say "6" means that each player has to play in the local area when the temperature drops under 6.

The thing is that kos typically destroy the independence of the local area of the ko and the rest of the board. The concepts of komaster and NTE are ways of taking account of the relevance of the rest of the board. With kos we cannot always rely upon the basic idea of miai values.

Miai values rely upon average territorial values. With a ko, strictly speaking there may not be an average value, and thus, no miai value in the basic sense, either. That is why Berlekamp talked about the mast values of kos.

And indeed, if NTE conditions apply, either player should play in the corner when the global temperature drops under 6. In addition, with complex kos such as this one, altering the conditions on the rest of the board is often done instead of playing in the local ko position.

And, as we have seen, with this ko the top three plays elsewhere may be considered as local. Kos destroy the independence of the board.

Bill Spight · **#903**

I have dubbed the ko plus other relevant regions of the board the ko ensemble.

Maybe I have goofed, but I think that the ko corner plus one humungous ko threat for Black makes Black komaster. Here is an SGF file.

The ko ensemble has a mast value of -1½, with each play gaining 6½ points on average.

Gérard TAILLE · **#904**

Bill Spight wrote:

I have dubbed the ko plus other relevant regions of the board the ko ensemble.

Maybe I have goofed, but I think that the ko corner plus one humungous ko threat for Black makes Black komaster. Here is an SGF file.

Oops why not the above sequence? I alaways proposed to play white tenuki in the corner just after having played my new move A17. That way white can save his group.

Bill Spight · **#905**

Very good, thanks.

Here is a new SGF file. Edited for correctness.

So the mast value of the ko ensemble is -5 points and the average gain per move is 3 points.

Edit: As pointed out later, this calculation does not give the value of the vertical mast, which is what the unqualified term, mast value, indicates.

Gérard TAILLE · **#906**

Bill Spight wrote:

Very good, thanks.

Here is a new SGF file. Edited for correctness.

So the average value of the ko ensemble is -5 points and the average gain per move is 3 points.

I do not understand how you count the ko variant

Click Here To Show Diagram Code: [go]$$W $$ --------------------- $$ | X 1 X O X X O O . | $$ | . X O O X X O O O | $$ | X . O X X X O O O | $$ | 2 O O X . X O O O | $$ | X O X X . X O O O | $$ | . X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

Unless the temperature is very low the answer :b2:

is very bad isn't it?
My feeling is that white must play in the corner as soon as she cannot afford to give up the corner. IOW I see a miai value far higher than yours and probably near from 6½. Are you sure white has better to play in the environment if temperature is between 3 and 6½ ?

Bill Spight · **#907**

Gérard TAILLE wrote:

Bill Spight wrote:

Very good, thanks.

Here is a new SGF file. Edited for correctness.

So the average value of the ko ensemble is -5 points and the average gain per move is 3 points.

I do not understand how you count the ko variant

Click Here To Show Diagram Code: [go]$$W $$ --------------------- $$ | X 1 X O X X O O . | $$ | . X O O X X O O O | $$ | X . O X X X O O O | $$ | 2 O O X . X O O O | $$ | X O X X . X O O O | $$ | . X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

Unless the temperature is very low the answer :b2:

is very bad isn't it?

It is sente, isn't it?

To find the local territorial count you play out the sente.

If Black plays elsewhere, so that White wins the ko with more local plays than Black, we cannot find a mast value fo the ko ensemble, because then White plays as many net local plays as when White plays first. If you want to consider a Black play elsewhere at this point, it must be part of the ko ensemble.

Gérard TAILLE wrote:

My feeling is that white must play in the corner as soon as she cannot afford to give up the corner. IOW I see a miai value far higher than yours and probably near from 6½. Are you sure white has better to play in the environment if temperature is between 3 and 6½ ?

When you can read the play out you don't need theory. Both thermography and the traditional way of estimating territory and the value of plays only promise estimates and heuristics. So whenever you ask me whether I am sure that a heuristic is right, regardless of the rest of the board, I have to say no.

But looking at this corner with no ko threats, we found that the three hottest positions probably belong in the ko ensemble. Maybe in this case the two hottest positions belong in the ko ensemble.

Gérard TAILLE · **#908**

Bill Spight wrote:

It is sente, isn't it?

To find the local territorial count you play out the sente.

I do dot understand Bill.
OC it is sente but that does not mean that you have to play it to find the territorial count.
Let's take a very simple example

Click Here To Show Diagram Code: [go]$$W $$ --------------------- $$ | . X O X . . . . . | $$ | X O O X . . . . . | $$ | . O X X . . . . . | $$ | . O X . . . . . . | $$ | X X X . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ ---------------------[/go]

Click Here To Show Diagram Code: [go]$$W $$ --------------------- $$ | 1 X O X . . . . . | $$ | X O O X . . . . . | $$ | . O X X . . . . . | $$ | 2 O X . . . . . . | $$ | X X X . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ ---------------------[/go]

After

the move

is sente but looks quite bad. In order to count the local territory will you assume this sente move or will you assume a ko fight?

Bill Spight · **#909**

Gérard TAILLE wrote:

Bill Spight wrote:

It is sente, isn't it?

To find the local territorial count you play out the sente.

I do dot understand Bill.
OC it is sente but that does not mean that you have to play it to find the territorial count.
Let's take a very simple example

Click Here To Show Diagram Code: [go]$$W $$ --------------------- $$ | . X O X . . . . . | $$ | X O O X . . . . . | $$ | . O X X . . . . . | $$ | . O X . . . . . . | $$ | X X X . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ ---------------------[/go]

Click Here To Show Diagram Code: [go]$$W $$ --------------------- $$ | 1 X O X . . . . . | $$ | X O O X . . . . . | $$ | . O X X . . . . . | $$ | 2 O X . . . . . . | $$ | X X X . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ ---------------------[/go]

After

the move

is sente but looks quite bad. In order to count the local territory will you assume this sente move or will you assume a ko fight?

It's a bad play at territorial scoring, because it gains nothing. {shrug} We do not play it for that reason.

Click Here To Show Diagram Code: [go]$$W White first $$ --------------------- $$ | 1 X O X . . . . . | $$ | X O O X . . . . . | $$ | 3 O X X . . . . . | $$ | . O X . . . . . . | $$ | X X X . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ ---------------------[/go]

Result: -4 in 2 plays by White.

Click Here To Show Diagram Code: [go]$$B Black first $$ --------------------- $$ | . X O X . . . . . | $$ | X O O X . . . . . | $$ | . O X X . . . . . | $$ | 1 O X . . . . . . | $$ | X X X . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ ---------------------[/go]

Result: +12 in 1 play by Black.

The ko has a mast value when

-4 + 2t = 12 - t, that is, when

t = 5⅓ , and the mast value, m, is

m = 6⅔

Bill Spight · **#910**

OK, let's at the simple gote, U = {u|-u}, u > 0, to the ko ensemble. U is not shown on the board.

Click Here To Show Diagram Code: [go]$$W White first, var. 1 $$ --------------------- $$ | . . . . X X O O . | $$ | 1 . O O X X O O O | $$ | . . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O a . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

= u

If White plays in the ko corner, Black replies in U when u > 1. That yields a sente sequence with the result, u - 8.

If White plays first in U, then the mast value is -5 - u in gote. Playing first in U dominates when

u - 8 ≥ -5 - u , that is, when

u ≥ 1½

Next, let Black play first.

Click Here To Show Diagram Code: [go]$$Wm10 Black first, var. 1 $$ --------------------- $$ | X 1 X O X X O O . | $$ | 3 X O O X X O O O | $$ | X 5 O X X X O O O | $$ | 2 O O X . X O O O | $$ | X O X X . X O O O | $$ | 4 X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

= u

Note that :b11:

gains 1 point at territorial go.

The result is u - 5 in 1 net Black play.

Click Here To Show Diagram Code: [go]$$Wm10 Black first, var. 2 $$ --------------------- $$ | X 1 X O X X O O . | $$ | 3 X O O X X O O O | $$ | X 5 O X X X O O O | $$ | . O O X . X O O O | $$ | X O X X . X O O O | $$ | 4 X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

= u

Note that :b13:

gains 1 point at territorial go.

The result is u - 6 in sente.

The play in U dominates when

u - 5 ≥ u - 6 , that is, always. :cool:

Last, suppose that Black plays in U first. Then White will play in the top left corner and the result will be u - 8 in sente. Obviously, variation 2 dominates that, as well.

Now to find the mast value of the ko ensemble.

When u > 1½ the mast value of the ko ensemble happens when

u - 5 = -5 - u , that is, when

u = 0 , that is, never.

So let 1½ > u > 1. The the mast value of the ko ensemble occurs when

u - 5 = u - 8, that is, never.

Maybe I have goofed again, but it seems like adding a simple gote to the ko ensemble does not produce a mast value for it. {shrug}

Give me a while and I'll try adding two simple gote to the ko ensemble.

Gérard TAILLE · **#911**

Before analysing your last post I give you my own analysis:

Click Here To Show Diagram Code: [go]$$W $$ --------------------- $$ | . . . . X X O O . | $$ | . . O O X X O O O | $$ | . . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O . . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

white plays first in the corner:

Click Here To Show Diagram Code: [go]$$W White first $$ --------------------- $$ | . . . . X X O O . | $$ | 1 . O O X X O O O | $$ | . . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O . . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

tenuki
scoreWhiteFirst = -7 + t

Black plays first in the corner and white saves his corner:

Click Here To Show Diagram Code: [go]$$B Black first, ko $$ --------------------- $$ | 5 2 7 8 X X O O . | $$ | 4 1 O O X X O O O | $$ | 3 . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O 6 . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

Click Here To Show Diagram Code: [go]$$Bcm9 Black first, ko $$ --------------------- $$ | X 2 X O X X O O . | $$ | 4 X O O X X O O O | $$ | X 6 O X X X O O O | $$ | 8 O O X . X O O O | $$ | 1 O X X . X O O O | $$ | 7 X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

tenuki

tenuki
scoreBlackFirstKo = -8 + 2t

Black plays first in the corner and white gives up his corner:

Click Here To Show Diagram Code: [go]$$B black first, white killed $$ --------------------- $$ | 5 2 7 9 X X O O . | $$ | 4 1 O O X X O O O | $$ | 3 . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O . . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

tenuki

tenuki

tenuki
scoreBlackFirstWhiteKilled = +18 - 3t

The three scores are:
scoreWhiteFirst = -7 + t
scoreBlackFirstKo = -8 + 2t
scoreBlackFirstWhiteKilled = +18 - 3t

Obviously scoreBlackFirstKo is not good for white if t > 1.
The two other scores have to be compared:
scoreWhiteFirst = scoreBlackFirstWhiteKilled <=>
-7 + t = +18 - 3t <=>
t = 6¼ and m = -¾

In the last sequence you can argue that :b9:

may be omitted because black's ko threat is still available. If it is playable then
scoreBlackFirstWhiteKilledBis = +18 - 2t and
scoreWhiteFirst = scoreBlackFirstWhiteKilledBis <=>
-7 + t = +18 - 2t <=>
t = 8⅓ and m = 1⅓

The miai value is probably somewhere between 6¼ and 8⅓.

Bill Spight · **#912**

Many thanks, Gérard.

Gérard TAILLE wrote:

Before analysing your last post I give you my own analysis:

Click Here To Show Diagram Code: [go]$$W $$ --------------------- $$ | . . . . X X O O . | $$ | . . O O X X O O O | $$ | . . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O . . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

white plays first in the corner:

Click Here To Show Diagram Code: [go]$$W White first $$ --------------------- $$ | . . . . X X O O . | $$ | 1 . O O X X O O O | $$ | . . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O . . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

tenuki
scoreWhiteFirst = -7 + t

I think you misremembered that the average value of the top left corner is -5. The average value for the ko ensemble is -5 - 3 = -8. Result: -8 + t.

Click Here To Show Diagram Code: [go]$$B Black first, var. 1 $$ --------------------- $$ | . . . 4 X X O O . | $$ | O . O O X X O O O | $$ | . . O X X X O O O | $$ | 2 O O X . X O O O | $$ | 1 O X X . X O O O | $$ | 3 X . . . X O . . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

Click Here To Show Diagram Code: [go]$$B Black first, var. 2 $$ --------------------- $$ | . 4 3 1 X X O O . | $$ | O . O O X X O O O | $$ | . . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | 2 X . . . X O . . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

Gérard TAILLE wrote:

Black plays first in the corner and white saves his corner:

Click Here To Show Diagram Code: [go]$$B Black first, ko $$ --------------------- $$ | 5 2 7 8 X X O O . | $$ | 4 1 O O X X O O O | $$ | 3 . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O 6 . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

Click Here To Show Diagram Code: [go]$$Bcm9 Black first, ko $$ --------------------- $$ | X 2 X O X X O O . | $$ | 4 X O O X X O O O | $$ | X 6 O X X X O O O | $$ | 8 O O X . X O O O | $$ | 1 O X X . X O O O | $$ | 7 X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

tenuki

tenuki
scoreBlackFirstKo = -8 + 2t

Again, your counting seems off by 1. :scratch:

White has 6 points of territory and has captured 4 stones, for -10, and Black has 1 point of territory and has captured 2 stones, for +3. Result -7 + 2t.

Gérard TAILLE wrote:

Black plays first in the corner and white gives up his corner:

Click Here To Show Diagram Code: [go]$$B black first, white killed $$ --------------------- $$ | 5 2 7 9 X X O O . | $$ | 4 1 O O X X O O O | $$ | 3 . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O . . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

tenuki

tenuki

tenuki
scoreBlackFirstWhiteKilled = +18 - 3t

Here we agree on the score.

The three scores are:
scoreWhiteFirst = -7 + t
scoreBlackFirstKo = -8 + 2t
scoreBlackFirstWhiteKilled = +18 - 3t

Gérard TAILLE wrote:

Obviously scoreBlackFirstKo is not good for white if t > 1.
The two other scores have to be compared:
scoreWhiteFirst = scoreBlackFirstWhiteKilled <=>
-7 + t = +18 - 3t <=>
t = 6¼ and m = -¾

That should be, I think,

countWhiteFirst = -8 + t
scoreBlackFirstKo = -7 + 2t
scoreBlackFirstWhiteKilled = +18 - 3t

When t > 1 then scoreBlackFirstKo is better for White than countWhiteFirst. That is, in the BlackFirstKo sequence Black has made a mistake or White has made a mistake in the countWhiteFirst sequence.

The temperature of indifference between the WhiteFirst sequence and the BlackFirstWhiteKilled sequence occurs when

-8 + t = +18 - 3t , that is, when

t = 6½.

Gérard TAILLE · **#913**

Bill Spight wrote:

Many thanks, Gérard.

Gérard TAILLE wrote:

Before analysing your last post I give you my own analysis:

Click Here To Show Diagram Code: [go]$$W $$ --------------------- $$ | . . . . X X O O . | $$ | . . O O X X O O O | $$ | . . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O . . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

white plays first in the corner:

Click Here To Show Diagram Code: [go]$$W White first $$ --------------------- $$ | . . . . X X O O . | $$ | 1 . O O X X O O O | $$ | . . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O . . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

tenuki
scoreWhiteFirst = -7 + t

I think you misremembered that the average value of the top left corner is -5. The average value for the ko ensemble is -5 - 3 = -8. Result: -8 + t.

Click Here To Show Diagram Code: [go]$$B Black first, var. 1 $$ --------------------- $$ | . . . 4 X X O O . | $$ | O . O O X X O O O | $$ | . . O X X X O O O | $$ | 2 O O X . X O O O | $$ | 1 O X X . X O O O | $$ | 3 X . . . X O . . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

Click Here To Show Diagram Code: [go]$$B Black first, var. 2 $$ --------------------- $$ | . 4 3 1 X X O O . | $$ | O . O O X X O O O | $$ | . . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | 2 X . . . X O . . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

Gérard TAILLE wrote:

Black plays first in the corner and white saves his corner:

Click Here To Show Diagram Code: [go]$$B Black first, ko $$ --------------------- $$ | 5 2 7 8 X X O O . | $$ | 4 1 O O X X O O O | $$ | 3 . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O 6 . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

Click Here To Show Diagram Code: [go]$$Bcm9 Black first, ko $$ --------------------- $$ | X 2 X O X X O O . | $$ | 4 X O O X X O O O | $$ | X 6 O X X X O O O | $$ | 8 O O X . X O O O | $$ | 1 O X X . X O O O | $$ | 7 X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

tenuki

tenuki
scoreBlackFirstKo = -8 + 2t

Again, your counting seems off by 1. :scratch:

White has 6 points of territory and has captured 4 stones, for -10, and Black has 1 point of territory and has captured 2 stones, for +3. Result -7 + 2t.

Gérard TAILLE wrote:

Black plays first in the corner and white gives up his corner:

Click Here To Show Diagram Code: [go]$$B black first, white killed $$ --------------------- $$ | 5 2 7 9 X X O O . | $$ | 4 1 O O X X O O O | $$ | 3 . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O . . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

tenuki

tenuki

tenuki
scoreBlackFirstWhiteKilled = +18 - 3t

Here we agree on the score.

The three scores are:
scoreWhiteFirst = -7 + t
scoreBlackFirstKo = -8 + 2t
scoreBlackFirstWhiteKilled = +18 - 3t

Gérard TAILLE wrote:

Obviously scoreBlackFirstKo is not good for white if t > 1.
The two other scores have to be compared:
scoreWhiteFirst = scoreBlackFirstWhiteKilled <=>
-7 + t = +18 - 3t <=>
t = 6¼ and m = -¾

That should be, I think,

countWhiteFirst = -8 + t
scoreBlackFirstKo = -7 + 2t
scoreBlackFirstWhiteKilled = +18 - 3t

When t > 1 then scoreBlackFirstKo is better for White than countWhiteFirst. That is, in the BlackFirstKo sequence Black has made a mistake or White has made a mistake in the countWhiteFirst sequence.

The temperature of indifference between the WhiteFirst sequence and the BlackFirstWhiteKilled sequence occurs when

-8 + t = +18 - 3t , that is, when

t = 6½.

Thank you for correcting my count Bill.
with the t = 6½ conclusion I am satisfied.
As we can see the situation with a black ko threat is very different. When no black ko threat white will not play in the corner (unless temperature is very low) but with one black ko threat white must play in the corner as soon as temperature drops under t = 6½.
BTW with more than one black ko threat, black is komaster and again white must play in the corner when temperature drops under t = 6½.
Finally with only one ko threat black is "almost" komaster isn't she?

Bill Spight · **#914**

Gérard TAILLE wrote:

Bill Spight wrote:

Many thanks, Gérard.

Gérard TAILLE wrote:

Before analysing your last post I give you my own analysis:

Click Here To Show Diagram Code: [go]$$W $$ --------------------- $$ | . . . . X X O O . | $$ | . . O O X X O O O | $$ | . . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O . . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

white plays first in the corner:

Click Here To Show Diagram Code: [go]$$W White first $$ --------------------- $$ | . . . . X X O O . | $$ | 1 . O O X X O O O | $$ | . . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O . . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

tenuki
scoreWhiteFirst = -7 + t

I think you misremembered that the average value of the top left corner is -5. The average value for the ko ensemble is -5 - 3 = -8. Result: -8 + t.

Click Here To Show Diagram Code: [go]$$B Black first, var. 1 $$ --------------------- $$ | . . . 4 X X O O . | $$ | O . O O X X O O O | $$ | . . O X X X O O O | $$ | 2 O O X . X O O O | $$ | 1 O X X . X O O O | $$ | 3 X . . . X O . . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

Click Here To Show Diagram Code: [go]$$B Black first, var. 2 $$ --------------------- $$ | . 4 3 1 X X O O . | $$ | O . O O X X O O O | $$ | . . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | 2 X . . . X O . . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

Gérard TAILLE wrote:

Black plays first in the corner and white saves his corner:

Click Here To Show Diagram Code: [go]$$B Black first, ko $$ --------------------- $$ | 5 2 7 8 X X O O . | $$ | 4 1 O O X X O O O | $$ | 3 . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O 6 . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

Click Here To Show Diagram Code: [go]$$Bcm9 Black first, ko $$ --------------------- $$ | X 2 X O X X O O . | $$ | 4 X O O X X O O O | $$ | X 6 O X X X O O O | $$ | 8 O O X . X O O O | $$ | 1 O X X . X O O O | $$ | 7 X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

tenuki

tenuki
scoreBlackFirstKo = -8 + 2t

Again, your counting seems off by 1. :scratch:

White has 6 points of territory and has captured 4 stones, for -10, and Black has 1 point of territory and has captured 2 stones, for +3. Result -7 + 2t.

Gérard TAILLE wrote:

Black plays first in the corner and white gives up his corner:

Click Here To Show Diagram Code: [go]$$B black first, white killed $$ --------------------- $$ | 5 2 7 9 X X O O . | $$ | 4 1 O O X X O O O | $$ | 3 . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O . . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

tenuki

tenuki

tenuki
scoreBlackFirstWhiteKilled = +18 - 3t

Here we agree on the score.

The three scores are:
scoreWhiteFirst = -7 + t
scoreBlackFirstKo = -8 + 2t
scoreBlackFirstWhiteKilled = +18 - 3t

Gérard TAILLE wrote:

Obviously scoreBlackFirstKo is not good for white if t > 1.
The two other scores have to be compared:
scoreWhiteFirst = scoreBlackFirstWhiteKilled <=>
-7 + t = +18 - 3t <=>
t = 6¼ and m = -¾

That should be, I think,

countWhiteFirst = -8 + t
scoreBlackFirstKo = -7 + 2t
scoreBlackFirstWhiteKilled = +18 - 3t

When t > 1 then scoreBlackFirstKo is better for White than countWhiteFirst. That is, in the BlackFirstKo sequence Black has made a mistake or White has made a mistake in the countWhiteFirst sequence.

The temperature of indifference between the WhiteFirst sequence and the BlackFirstWhiteKilled sequence occurs when

-8 + t = +18 - 3t , that is, when

t = 6½.

Thank you for correcting my count Bill.
with the t = 6½ conclusion I am satisfied.
As we can see the situation with a black ko threat is very different. When no black ko threat white will not play in the corner (unless temperature is very low) but with one black ko threat white must play in the corner as soon as temperature drops under t = 6½.
BTW with more than one black ko threat, black is komaster and again white must play in the corner when temperature drops under t = 6½.
Finally with only one ko threat black is "almost" komaster isn't she?

I am sorry, my statement about one player or other, given the results, having made a mistake, is wrong. :oops:

After

Black can kill the corner without playing :b9:

, so

is a mistake. Black should wait until White eliminates the ko threat to play :b9:

. That yields scoreBlackFirstWhiteKilled = +19 - 2t. The temperature of indifference occurs when

-8 + t = +19 - 2t , that is, when

t = 9.

When should :w6:

eliminate the ko threat after :b5:

? If, indeed, White's best play afterwards is the sequence in BlackFirstKo, it is when

-7 + 2t < +19 - 2t , that is, when

t < 6½.

So, given that assumption, if :w6:

does not eliminate the ko threat, :b7:

should not kill the corner unless t < 9, and :w6:

should not eliminate the ko threat until t < 6½. Between those two temperatures Black wins the ko, even though White can prevent it, a case of tunneling.

Bill Spight · **#915**

Our discussion of Gérard's last post has revealed that the question of :w6:

filling the ko threat is open with a larger ko ensemble, so let me revisit it when we add a simple gote, U = {u|-u}, u > 0.

Click Here To Show Diagram Code: [go]$$B Black first, var. 1 $$ --------------------- $$ | 5 2 7 9 X X O O . | $$ | 4 1 O O X X O O O | $$ | 3 . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O 8 . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

= -u

Result: +19 - u + t

There are a number of transpositions to get that result.

Click Here To Show Diagram Code: [go]$$B Black first, var. 1 $$ --------------------- $$ | 5 2 7 9 X X O O . | $$ | 4 1 O O X X O O O | $$ | 3 . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O 8 . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

= -u

Click Here To Show Diagram Code: [go]$$B Black first, var. 2 $$ --------------------- $$ | 5 2 7 8 X X O O . | $$ | 4 1 O O X X O O O | $$ | 3 . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O 6 . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

= u

Click Here To Show Diagram Code: [go]$$Wm10 Black first, var. 2 $$ --------------------- $$ | X 1 X O X X O O . | $$ | 3 X O O X X O O O | $$ | X 5 O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

= u

Result when t > 0: u - 8 + 3t

Alternate results after :b7:

.

Click Here To Show Diagram Code: [go]$$Wm10 Black first, var. 2 $$ --------------------- $$ | X 1 X O X X O O . | $$ | 3 X O O X X O O O | $$ | X 5 O X X X O O O | $$ | . O O X . X O O O | $$ | 2 O X X . X O O O | $$ | . X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

= u

Click Here To Show Diagram Code: [go]$$Wm10 Black first, var. 2 $$ --------------------- $$ | X 1 X O X X O O . | $$ | 3 X O O X X O O O | $$ | X 5 O X X X O O O | $$ | . O O X . X O O O | $$ | 2 O X X . X O O O | $$ | . X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

= u

Result when t > 1: u - 7 + 2t

Click Here To Show Diagram Code: [go]$$Wm10 Black first, var. 3 $$ --------------------- $$ | X 1 X O X X O O . | $$ | 3 X O O X X O O O | $$ | X 5 O X X X O O O | $$ | 4 O O X . X O O O | $$ | 2 O X X . X O O O | $$ | 6 X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

= u

Result when t > 1: u - 6 + t

OC, the best result when Black takes U and t > 1 is the first.

So it looks like, even with the humungous threat, we want to add 3 simple gote to the ko ensemble, U = {u|-u}, V = {v|-v}, and W = {w|-w}, u ≥ v ≥ w > 1.

Gérard TAILLE · **#916**

Bill Spight wrote:

Our discussion of Gérard's last post has revealed that the question of :w6:

filling the ko threat is open with a larger ko ensemble, so let me revisit it when we add a simple gote, U = {u|-u}, u > 0.

Click Here To Show Diagram Code: [go]$$B Black first, var. 1 $$ --------------------- $$ | 5 2 7 9 X X O O . | $$ | 4 1 O O X X O O O | $$ | 3 . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O 8 . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

= -u

Result: +19 - u + t

There are a number of transpositions to get that result.

Click Here To Show Diagram Code: [go]$$B Black first, var. 1 $$ --------------------- $$ | 5 2 7 9 X X O O . | $$ | 4 1 O O X X O O O | $$ | 3 . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O 8 . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

= -u

Click Here To Show Diagram Code: [go]$$B Black first, var. 2 $$ --------------------- $$ | 5 2 7 8 X X O O . | $$ | 4 1 O O X X O O O | $$ | 3 . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O 6 . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

= u

Click Here To Show Diagram Code: [go]$$Wm10 Black first, var. 2 $$ --------------------- $$ | X 1 X O X X O O . | $$ | 3 X O O X X O O O | $$ | X 5 O X X X O O O | $$ | . O O X . X O O O | $$ | 2 O X X . X O O O | $$ | . X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

= u

your move

= u and the following :w10:

seem to me bad moves.

Click Here To Show Diagram Code: [go]$$B $$ --------------------- $$ | X . X O X X O O . | $$ | . X O O X X O O O | $$ | X . O X X X O O O | $$ | . O O X . X O O O | $$ | a O X X . X O O O | $$ | . X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

The point is to compare the black hane at "a" immediatly or one move later as you suggest.
Let's take the environment g1, g2, g3, ...

Click Here To Show Diagram Code: [go]$$B Black begins by hane $$ --------------------- $$ | X 2 X O X X O O . | $$ | 4 X O O X X O O O | $$ | X 6 O X X X O O O | $$ | . O O X . X O O O | $$ | 1 O X X . X O O O | $$ | . X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

takes g1

takes g2

takes g3
scoreHaneImmediately = -7 + g1 + g2 + g3 - g4 + g5 - g6 ...

Click Here To Show Diagram Code: [go]$$B Black plays hane later $$ --------------------- $$ | X 4 X O X X O O . | $$ | 6 X O O X X O O O | $$ | X 8 O X X X O O O | $$ | . O O X . X O O O | $$ | 3 O X X . X O O O | $$ | . X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

takes g1

takes g2 (the point!)
:b5:

takes g3

takes g4

takes g5

scoreHanelater = -7 + g1 - g2 + g3 + g4 + g5 - g6 ...

scoreHaneImmediately - scoreHanelater = -7 + g1 + g2 + g3 - g4 + g5 - g6 ... - -7 + g1 - g2 + g3 + g4 + g5 - g6 ... = 2(g2 -g4)

You see that by delaying black hane you lose 2(g2 -g4) points.
I perfectly know that you may have g2=g4 but for a technical point of view delaying the hane looks bad and it is dominated by the immediat hane.

Bill Spight wrote:

So it looks like, even with the humungous threat, we want to add 3 simple gote to the ko ensemble, U = {u|-u}, V = {v|-v}, and W = {w|-w}, u ≥ v ≥ w > 1.

Click Here To Show Diagram Code: [go]$$W $$ --------------------- $$ | . X O X . . . . . | $$ | X O O X . . . . . | $$ | . O X X . . . . . | $$ | . O X . . . . . . | $$ | X X X . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ ---------------------[/go]

In this very simple ko, with the same arguement, why don't you want to add to the ko ensemble the simple gote U = {u|-u} ?

When your are facing a ko with a non ideal environment it is obviously a good idea to add some simple gote in order deal with such special environment. In our case why not considering simply an ideal environment? OC if you encounter a real difficulty you can always change your mind and add simple gote to the ko ensemble. Is it the case here or do you want really to study non ideal environment for this position?

Bill Spight · **#917**

Gérard TAILLE wrote:

Bill Spight wrote:

Our discussion of Gérard's last post has revealed that the question of :w6:

filling the ko threat is open with a larger ko ensemble, so let me revisit it when we add a simple gote, U = {u|-u}, u > 0.

Click Here To Show Diagram Code: [go]$$B Black first, var. 1 $$ --------------------- $$ | 5 2 7 9 X X O O . | $$ | 4 1 O O X X O O O | $$ | 3 . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O 8 . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

= -u

Result: +19 - u + t

There are a number of transpositions to get that result.

Click Here To Show Diagram Code: [go]$$B Black first, var. 1 $$ --------------------- $$ | 5 2 7 9 X X O O . | $$ | 4 1 O O X X O O O | $$ | 3 . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O 8 . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

= -u

Click Here To Show Diagram Code: [go]$$B Black first, var. 2 $$ --------------------- $$ | 5 2 7 8 X X O O . | $$ | 4 1 O O X X O O O | $$ | 3 . O X X X O O O | $$ | . O O X . X O O O | $$ | . O X X . X O O O | $$ | . X . . . X O 6 . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

= u

Click Here To Show Diagram Code: [go]$$Wm10 Black first, var. 2 $$ --------------------- $$ | X 1 X O X X O O . | $$ | 3 X O O X X O O O | $$ | X 5 O X X X O O O | $$ | . O O X . X O O O | $$ | 2 O X X . X O O O | $$ | . X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

= u

your move

= u and the following :w10:

seem to me bad moves.

Click Here To Show Diagram Code: [go]$$B $$ --------------------- $$ | X . X O X X O O . | $$ | . X O O X X O O O | $$ | X . O X X X O O O | $$ | . O O X . X O O O | $$ | a O X X . X O O O | $$ | . X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

The point is to compare the black hane at "a" immediatly or one move later as you suggest.
Let's take the environment g1, g2, g3, ...

Click Here To Show Diagram Code: [go]$$B Black begins by hane $$ --------------------- $$ | X 2 X O X X O O . | $$ | 4 X O O X X O O O | $$ | X 6 O X X X O O O | $$ | . O O X . X O O O | $$ | 1 O X X . X O O O | $$ | . X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

takes g1

takes g2

takes g3
scoreHaneImmediately = -7 + g1 + g2 + g3 - g4 + g5 - g6 ...

Click Here To Show Diagram Code: [go]$$B Black plays hane later $$ --------------------- $$ | X 4 X O X X O O . | $$ | 6 X O O X X O O O | $$ | X 8 O X X X O O O | $$ | . O O X . X O O O | $$ | 3 O X X . X O O O | $$ | . X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

takes g1

takes g2 (the point!)
:b5:

takes g3

takes g4

takes g5

scoreHanelater = -7 + g1 - g2 + g3 + g4 + g5 - g6 ...

scoreHaneImmediately - scoreHanelater = -7 + g1 + g2 + g3 - g4 + g5 - g6 ... - -7 + g1 - g2 + g3 + g4 + g5 - g6 ... = 2(g2 -g4)

You see that by delaying black hane you lose 2(g2 -g4) points.
I perfectly know that you may have g2=g4 but for a technical point of view delaying the hane looks bad and it is dominated by the immediat hane.

You make some good points.

But, as I said before, we have different objectives. I am looking to evaluate the ko ensemble. Without adding any simple gote to the one with just the ko corner and the humungous threat, I already did so, and maybe that's good enough. It's a 3 point Black sente.

(Edit: That may not be so. I have not bothered to work out the thermograph the old fashioned way. I think I better just do that. It would have saved a lot of time, but not been as interesting. :lol:

) Adding U it is surprising how many sequences lead to no mast at a non-negative temperature. I have been playing around with adding two simple gote. It is an improvement, but still not simple. Maybe it's just not a great idea. {shrug}

I started off using von Neuman game theory and an environment of simple gote, but frankly, in trying to find a mast value for the ko ensemble, I did not work anything out from that perspective. I appreciate your pointing out what can be gleaned from that approach.

Bill Spight wrote:

So it looks like, even with the humungous threat, we want to add 3 simple gote to the ko ensemble, U = {u|-u}, V = {v|-v}, and W = {w|-w}, u ≥ v ≥ w > 1.

Click Here To Show Diagram Code: [go]$$W $$ --------------------- $$ | . X O X . . . . . | $$ | X O O X . . . . . | $$ | . O X X . . . . . | $$ | . O X . . . . . . | $$ | X X X . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ ---------------------[/go]

In this very simple ko, with the same arguement, why don't you want to add to the ko ensemble the simple gote U = {u|-u} ?[/quote]

In the late 1980s I struggled with finding the best play for what Berlekamp called hyperactive ko positions, with an environment of simple gote and simple ko threats. They are deucedly difficult. I often resorted to finite environment, adding one gote or one ko threat at a time. Even so, they quickly became intractable. Since learning CGT and Berlekamp's komaster analysis, things which were difficult became easy. I have avoided complicating things.

So I find it very interesting how, with this particular ko position, it has seemed like a good idea to add a few gote to the ko ensemble. I appreciate your insights. :bow:

But in general I try to avoid complications.

KISS = keep it simple, sister.

As for the admittedly simple ko above, it is easy to evaluate without reference to any gote.

Gérard TAILLE · **#918**

Yes Bill, we have to make our maximum to keep things as simple as possible.

When I analyse a position in order to discover the best moves, the miai value and the mast value, the first phase consists of finding the best sequences. Here my view is that we must make our maximum to play the technically best moves. We must avoid technically bad moves as for example a bad order of the moves. In order to reach this goal I prefer to use a rich environment ε, 2ε, 3ε, 4ε ...
That way I can see a difference between the sequences
g1 + g2 + g3 - g4 + g5 - g6 ... and g1 - g2 + g3 + g4 + g5 - g6 ... = 2(g2 -g4) = 4ε
As soon as the best sequence has been discovered then I prefer to use the usual ideal environment to give a result as simple as possible.

OC if I want to show a small particularity of the position, depending of the environment, then I can build a complete environment.

What is your own approach Bill?

Bill Spight · **#919**

First, to all readers, let me apologize for any crankiness and resulting errors recently. I am not well, and have not been for some time. It's not too serious, but it has affected my motivation and concentration.

Bill Spight · **#920**

Gérard TAILLE wrote:

Yes Bill, we have to make our maximum to keep things as simple as possible.

When I analyse a position in order to discover the best moves, the miai value and the mast value, the first phase consists of finding the best sequences. Here my view is that we must make our maximum to play the technically best moves. We must avoid technically bad moves as for example a bad order of the moves. In order to reach this goal I prefer to use a rich environment ε, 2ε, 3ε, 4ε ...
That way I can see a difference between the sequences
g1 + g2 + g3 - g4 + g5 - g6 ... and g1 - g2 + g3 + g4 + g5 - g6 ... = 2(g2 -g4) = 4ε
As soon as the best sequence has been discovered then I prefer to use the usual ideal environment to give a result as simple as possible.

OC if I want to show a small particularity of the position, depending of the environment, then I can build a complete environment.

What is your own approach Bill?

My main concern these days is spreading and promoting thermography in go. Thermography was invented by Conway in the 1970s and published in On Numbers and Games. A friend lent me a copy and thought that thermography might be of interest in go. Then thermography was defined in terms of applying a tax to plays. It seemed to produce the same evaluations of go positions and plays as methods that go players already used — I was unaware of the problems with complex ko positions at that time —, so I did not see any benefit from it.

That changed for me when I attended a lecture by Berlekamp in 1994 or 5 in which he presented his komaster theory. Despite the fact that it left open the question of whether the conditions for komaster were met in actual play, it provided a considerably more tractable theory for evaluating complex ko positions than the ko theory I had developed. My theory included all of the environment in the ko ensemble. The problem with doing that is that to evaluate a ko you have to read out the whole board. But, OC, if you can do that you don't need any theory. :lol:

I joined a small group consisting of Berlekamp, some of his students and former students, and visiting scholars, and myself, which mainly studied komaster theory. At first I solved problems by opining correct play and then drawing the thermograph from that. This irked Berlekamp, who was around 3 kyu, because he contended that thermography provided a way of finding correct play. He was right, OC. Thermographic lines generated by incorrect play do not appear in the final thermograph.

At temperature 0, where the game is played out, thermography indicates correct play, but that is guaranteed only by exhaustive search, or by perhaps other means of proving correct play. (If there is an encore, thermography may apply below temperature 0, but in go this is highly dependent upon the rules.) What thermography does is to provide correct play at each temperature. A play or line of play may be incorrect at one temperature and correct at another. Any play, given otherwise correct play, that produces the best result at a given temperature for the player, will indicate a point on the thermograph at that temperature.

So, for instance,

Click Here To Show Diagram Code: [go]$$W White to play $$ --------------------- $$ | X 1 X O X X O O . | $$ | 3 X O O X X O O O | $$ | X 5 O X X X O O O | $$ | 4 O O X . X O O O | $$ | X O X X . X O O O | $$ | 2 X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

This line of play gives the best result for Black at or below temperature 1 and will thus indicate the wall of the thermograph in that temperature range.

Click Here To Show Diagram Code: [go]$$W White to play $$ --------------------- $$ | X 1 X O X X O O . | $$ | 3 X O O X X O O O | $$ | X 5 O X X X O O O | $$ | . O O X . X O O O | $$ | X O X X . X O O O | $$ | . X . . . X O O . | $$ | . X . . . X X O O | $$ | X X . . . . X X X | $$ | . . . . . . . . . | $$ ---------------------[/go]

,

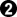
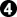
elsewhere (in the environment)

This result is 2 points worse for Black on the board than the previous result, so it is preferable when t > 1.

Also,

Click Here To Show Diagram Code: [go]$$W White to play $$ --------------------- $$ | 1 X O X . . . . . | $$ | X O O X . . . . . | $$ | 3 O X X . . . . . | $$ | 2 O X . . . . . . | $$ | X X X . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ ---------------------[/go]

This is the best Black can do at temperature 0, and indicates the wall of the thermograph at that temperature.

Click Here To Show Diagram Code: [go]$$W White to play $$ --------------------- $$ | 1 X O X . . . . . | $$ | X O O X . . . . . | $$ | 3 O X X . . . . . | $$ | C O X . . . . . . | $$ | X X X . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ | . . . . . . . . . | $$ ---------------------[/go]

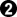
elsewhere

OC, above temperature 0 Black will not play :b2:

.

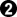
At temperature 0 one player or other will fill the dame. Doing so did not change the score, OC, before the Japanese 1989 rules, which scores the White group as 0 if the dame, :ec:

, is unfilled. In fact, the Japanese used to be quite proud of not filling the dame. (The J89 rules included a loophole which allowed players to continue their practice of leaving dame unfilled before scoring. But that has led to problems since then.)

This 'n' that

Who is online