These "have a loop" and "have an advantageous loop" doesn't seem clear enough. Do sequences with double passes count as loop? If no, how to "have advantageous loop" if opponent passes (once) after my pass? If yes, would a sole double ko seki make a loop? Maybe an advantageous loop even, breaking it?

https://lifein19x19.com/viewtopic.php?p=266763#p266763


Needs some editing. is utilised twice.

_________________
The really most difficult Go problem ever: https://igohatsuyoron120.de/index.htm
Igo Hatsuyōron #120 (really solved by KataGo)

https://lifein19x19.com/viewtopic.php?p=266754#p266754


Needs some editing. One Black stone is missing.

_________________
The really most difficult Go problem ever: https://igohatsuyoron120.de/index.htm
Igo Hatsuyōron #120 (really solved by KataGo)

I like such questions Jann because they adresse directly my ideas rather then a formal text on which I need help to find the best english wording.
So let's consider my ideas and I will see later how to improve my formal text, maybe with your help.

The only basic question you have to answer is the following : can a player prevents her opponent to make infinite passes? If the answer is YES it looks an advantage for the player doesn't it? Surprisingly a go player is generally able to answer this question very quickly and may even consider such question as obvious

Let's take the simple double ko

Click Here To Show Diagram Code

[go]$$B
$$ ---------------------
$$ | . . . X O X . X . |
$$ | . . . X O O X X X |
$$ | . . . X O . O X O |
$$ | . . . X O O O O . |
$$ | . . . X X X X O O |
$$ | . . . . . . X X X |
$$ | . . . . . . . . . |
$$ | . . . . . . . . . |
$$ | . . . . . . . . . |
$$ ---------------------[/go]

Can white prevents black to make infinite passes? Obviously the answer is NO isn't it?
Can black prevents white to make infinite passes? Obviously the answer is still NO?
The situation appears symmetrical => no advantageous loop.

Click Here To Show Diagram Code

[go]$$W
$$ -----------------
$$ | . X X X X X X |
$$ | X X . X O X X |
$$ | O O X O . O O |
$$ | . O O O O O O |
$$ | O X X X X X X |
$$ | X X . . . X . |
$$ | . . . . . X . |
$$ -----------------[/go]

Can white prevents black to make infinite passes? Obviously the answer is NO?
Can black prevents white to make infinite passes? This time the answer is YES, isn't it?
The situation is not symmetrical => black has an advantageous loop.

Considering your questions the point is to avoid mixing the two questions above. It is true that if black plays a sequence showing infinite passes for black then white would have also infinite passes. But that was not the questions above.

Click Here To Show Diagram Code

[go]$$W
$$ -----------------
$$ | X X X X X X X |
$$ | . X . X . X O |
$$ | O O X O X O . |
$$ | O O O O O O O |
$$ | X X X X X X X |
$$ | . . . . . X . |
$$ | . . . . . X . |
$$ -----------------[/go]

Can white prevents black to make infinite passes? Obviously the answer is YES?
Can black prevents white to make infinite passes? the answer is still YES?
The situation appears symmetrical => no advantageous loop.

Additonnal comment on these three examples:
In the first one the answers to the two basic questions are NO, NO => generally seki in common GO language or NO TERRITORY in my langage
In the second example the answers to the two basic questions are NO, YES => generally alive stones against dead stones in common GO language or TERRITORY in my langage
In the third example the answer to the two basic questions are YES, YES => generally seki in common GO language or NO TERRITORY in my langage. BTW in normal play this situation is a NO RESULT game.

Let's try to apply this stuff to monshine life:

Click Here To Show Diagram Code

[go]$$B
$$ ---------------------
$$ | . . . X O X . X . |
$$ | . . . X O O X X X |
$$ | . . . X O . O X O |
$$ | . . . X O O O O . |
$$ | . . . X X X X O O |
$$ | . . . . . . X X X |
$$ | X X X X . . . . . |
$$ | O O O X X . . . . |
$$ | . O . O X . . . . |
$$ ---------------------[/go]

Click Here To Show Diagram Code

[go]$$B
$$ ---------------------
$$ | C C C B O X . X . |
$$ | C C C B O O X X X |
$$ | C C C B O . O X O |
$$ | C C C B O O O O . |
$$ | C C C B B B B O O |
$$ | C C C C C C B B B |
$$ | B B B B C C C C C |
$$ | W W W B B C C C C |
$$ | C W C W B C C C C |
$$ ---------------------[/go]

Assume black claims for a black territory for the marked set of locations above then it follows:

Click Here To Show Diagram Code

[go]$$W
$$ ---------------------
$$ | . . . X O X 1 X 3 |
$$ | . . . X O O X X X |
$$ | . . . X O . O X O |
$$ | . . . X O O O O . |
$$ | . . . X X X X O O |
$$ | . . . . . . X X X |
$$ | X X X X . . . . . |
$$ | O O O X X . . . . |
$$ | 4 O 2 O X . . . . |
$$ ---------------------[/go]

=> it is black territory

Now assume black is more greedy and claim a black territory covering all the board. What will happen?

Click Here To Show Diagram Code

[go]$$W pass
$$ ---------------------
$$ | . . . X O 6 1 X . |
$$ | . . . X O O X X X |
$$ | . . . X O . O X 5 |
$$ | . . . X O O O O 2 |
$$ | . . . X X X X O O |
$$ | . . . . . . X X X |
$$ | X X X X . . . . . |
$$ | O O O X X . . . . |
$$ | . O 4 7 X . . . . |
$$ ---------------------[/go]

white, showing the loop above ask the two basic questions:
Can white prevents black to make infinite passes? Obviously the answer is NO?
Can black prevents white to make infinite passes? The answer is YES, isn't it?
The situation is not symmetrical => black has an advantageous loop.
=> black is allowed to request "permenantly prohibited" ko. The game continue by

Click Here To Show Diagram Code

[go]$$Wm9 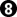pass pass
$$ ---------------------
$$ | . . . X O X 3 X . |
$$ | . . . X O O X X X |
$$ | . . . X O . O X O |
$$ | . . . X O O O O 2 |
$$ | . . . X X X X O O |
$$ | . . . . . . X X X |
$$ | X X X X . . . . . |
$$ | O O O X X . . . . |
$$ | . O . O X . . . . |
$$ ---------------------[/go]

and now pass and at the same time black requests the previous white ko capture at becomes a permanently prohibited ko. As a consequence you see white can capture all white stones => all the board is black territory.

OC this result is wrong but where is the mistake?
In fact white appears to be herself to greedy by trying to save all her stones. The mistaken move is (trying to save white stones at the bottom though they cannot be saved). Instead white should simply pass. That way the answer to the question
can black prevents white to make infinite passes?
is now NO and there are no advantageous loop!
Surely black can capture white stone at the bottom but not the white stones in the double ko
=> the all board is not black territory.
As usual everything must be made during confirmation phase to find the perfect play.

yes Cassandra, thank you. It's done.

Thank you again Cassandra. It is true. It's done now.

Is it simply a wording problem or it is a problem on the procedure itself?
BTW I did not use the wording "cycle" because for me a cycle is a sequence which is repeat indefinitly without any change. In that sense a cycle is only a particular case of loop.

Interesting project.

I'm not sure if
"2) the outside border of this set is only made of stones of the opponent or is empty"
really does what it's supposed to do (or if I don't quite understand it yet).

Click Here To Show Diagram Code

[go]$$B
$$ -----------------
$$ | . W W W W W W |
$$ | B B B B B B B |
$$ | . . . . . . . |
$$ | O O O O O O O |
$$ | . . . . . O . |
$$ | . . . . . O O |
$$ | . . . . . O . |
$$ -----------------[/go]

Is the marked set of locations a black territory?
if so, with what score?

In my understanding (visualise a solidly connected triple-ko, for example):

Click Here To Show Diagram Code

[go]$$B Loop
$$ +-------------------+
$$ | . . . . . . . . . |
$$ | . . . . X . . . . |
$$ | . O . . . . . O . |
$$ | . . . . . . . . . |
$$ | . . . . . . . . . |
$$ | . X . . . . . X . |
$$ | . . . . O . . . . |
$$ | . . . . . . . . . |
$$ | . . . . . . . . . |
$$ +-------------------+
$$ {AR F8 G7}
$$ {AR H6 H5}
$$ {AR G4 F3}
$$ {AR D3 C4}
$$ {AR B5 B6}
$$ {AR C7 D8}[/go]

A loop, once started, has no end. It's like walking on the circumference of a circle.

Click Here To Show Diagram Code

[go]$$B Cycle #1
$$ +-------------------+
$$ | . . . . . . . . . |
$$ | . . . . 1 . . . . |
$$ | . 6 . . . . . 2 . |
$$ | . . . . . . . . . |
$$ | . . . . . . . . . |
$$ | . 5 . . . . . 3 . |
$$ | . . . . 4 . . . . |
$$ | . . . . . . . . . |
$$ | . . . . . . . . . |
$$ +-------------------+
$$ {AR F8 G7}
$$ {AR H6 H5}
$$ {AR G4 F3}
$$ {AR D3 C4}
$$ {AR B5 B6}[/go]

First walk on the complete circumference of a circle. We get infinitely close to the starting point without reaching it.

Click Here To Show Diagram Code

[go]$$Bm7 Cycle #2
$$ +-------------------+
$$ | . . . . . . . . . |
$$ | . . . . 1 . . . . |
$$ | . 6 . . . . . 2 . |
$$ | . . . . . . . . . |
$$ | . . . . . . . . . |
$$ | . 5 . . . . . 3 . |
$$ | . . . . 4 . . . . |
$$ | . . . . . . . . . |
$$ | . . . . . . . . . |
$$ +-------------------+
$$ {AR F8 G7}
$$ {AR H6 H5}
$$ {AR G4 F3}
$$ {AR D3 C4}
$$ {AR B5 B6}[/go]

A tiny additional jump brought us to the initial starting point. It follows the second walk on the complete cirumfence.
Ad infinitum ...

############################

Just looked at your posting again. Probably I found the reason for our misunderstanding:


This is what I intended ( ) to write. Seems that it was too deep in the night...

_________________
The really most difficult Go problem ever: https://igohatsuyoron120.de/index.htm
Igo Hatsuyōron #120 (really solved by KataGo)

I do not understand what you are trying to say. Please explain!

Robert, I just tried to answer Jann questions (maybe I missed Jann point ).
These "have a loop" and "have an advantageous loop" doesn't seem clear enough. Do sequences with double passes count as loop? If no, how to "have advantageous loop" if opponent passes (once) after my pass? If yes, would a sole double ko seki make a loop? Maybe an advantageous loop even, breaking it?

I am not quite sure what additional information you want. Maybe I can clarify why I invented this "advantageous loop".
When you take a set of positions with potential loop (typically with three kos) the results for these positions given by J89 or J2003 or any traditionnal japonese rules depend clearly of the specific position. The work I have done was to try to find a particularity which can tell me if the result will be territory or a seki. I hoped and I was alomost convinced that such particularity must exist to explain the logic of japonese rules and result expected.
The result of my search is : yes this particularity is simply the answer to the two questions:
Can white prevents black to make infinite passes?
Can black prevents white to make infinite passes?
If the answers to these two questions are not the same then, for all examples I studied, the result will be dead versus alive stones (using common GO language) and the answer to the two questions tell us which side is in the best position. If the answers to these two questions are the same then, for all examples I studied, the result will be seki, neither side having an advantage.
In order to reach a result as close as possible to the expected result my view was simply to introduce these two questions within confirmation phase.
OC the exact wording has to be studied carefully but this is the idea.

Click Here To Show Diagram Code

[go]$$W
$$ -----------------
$$ | . X X X X X X |
$$ | X X . X O X X |
$$ | O O X O . O O |
$$ | . O O O O O O |
$$ | O X X X X X X |
$$ | X X . . . X . |
$$ | . . . . . X . |
$$ -----------------[/go]

Can White prevent Black from making infinite passes?

Click Here To Show Diagram Code

[go]$$W
$$ -----------------
$$ | . X X X X X X |
$$ | X X 1 X O X X |
$$ | O O X O 2 O O |
$$ | . O O O O O O |
$$ | O X X X X X X |
$$ | X X . . . X . |
$$ | . . . . . X . |
$$ -----------------[/go]

Click Here To Show Diagram Code

[go]$$W pass
$$ -----------------
$$ | . X X X X X X |
$$ | X X O X 5 X X |
$$ | O O 6 O X O O |
$$ | . O O O O O O |
$$ | O X X X X X X |
$$ | X X . . . X . |
$$ | . . . . . X . |
$$ -----------------[/go]

Click Here To Show Diagram Code

[go]$$Wm9 pass
$$ -----------------
$$ | . X X X X X X |
$$ | X X 1 X O X X |
$$ | O O X O 2 O O |
$$ | . O O O O O O |
$$ | O X X X X X X |
$$ | X X . . . X . |
$$ | . . . . . X . |
$$ -----------------[/go]

Variation:

Click Here To Show Diagram Code

[go]$$W
$$ -----------------
$$ | . X X X X X X |
$$ | X X O X 5 X X |
$$ | O O 6 O X O O |
$$ | 4 O O O O O O |
$$ | O X X X X X X |
$$ | X X . . . X . |
$$ | . . . . . X . |
$$ -----------------[/go]

Click Here To Show Diagram Code

[go]$$W
$$ -----------------
$$ | . X X X X X X |
$$ | X X . X O X X |
$$ | O O X O . O O |
$$ | X O O O O O O |
$$ | 7 X X X X X X |
$$ | X X . . . X . |
$$ | . . . . . X . |
$$ -----------------[/go]

Click Here To Show Diagram Code

[go]$$Wm9 pass
$$ -----------------
$$ | . X X X X X X |
$$ | X X 1 X O X X |
$$ | O O X O 2 O O |
$$ | . O O O O O O |
$$ | O X X X X X X |
$$ | X X . . . X . |
$$ | . . . . . X . |
$$ -----------------[/go]

Click Here To Show Diagram Code

[go]$$Wm9 pass
$$ -----------------
$$ | . X X X X X X |
$$ | X X O X 5 X X |
$$ | O O 6 O X O O |
$$ | . O O O O O O |
$$ | O X X X X X X |
$$ | X X . . . X . |
$$ | . . . . . X . |
$$ -----------------[/go]

see main line...

#############################
#############################

Can Black prevent White from making infinite passes?

Click Here To Show Diagram Code

[go]$$B
$$ -----------------
$$ | . X X X X X X |
$$ | X X 2 X O X X |
$$ | O O X O 1 O O |
$$ | 3 O O O O O O |
$$ | O X X X X X X |
$$ | X X . . . X . |
$$ | . . . . . X . |
$$ -----------------[/go]

are atari

Click Here To Show Diagram Code

[go]$$B
$$ -----------------
$$ | . X X X X X X |
$$ | X X O X 4 X X |
$$ | O O 5 O X O O |
$$ | X O O O O O O |
$$ | 6 X X X X X X |
$$ | X X . . . X . |
$$ | . . . . . X . |
$$ -----------------[/go]

is atari.

Click Here To Show Diagram Code

[go]$$B
$$ -----------------
$$ | . X X X X X X |
$$ | X X 8 X O X X |
$$ | O O X O 7 O O |
$$ | 9 O O O O O O |
$$ | O X X X X X X |
$$ | X X . . . X . |
$$ | . . . . . X . |
$$ -----------------[/go]

are atari.
Ad infinitum...

_________________
The really most difficult Go problem ever: https://igohatsuyoron120.de/index.htm
Igo Hatsuyōron #120 (really solved by KataGo)

I understand Cassandra and I agree with you for "simple" 3 kos positions. I just try to be more general, including position with 4 kos in which it is difficult to identify what the length of a cycle could be. In my GT rule I would like to take into all types of loops and not only 3 kos positions.

Click Here To Show Diagram Code

[go]$$W
$$ -----------------
$$ | X X X X X X X |
$$ | . X . X . X O |
$$ | O O X O X O . |
$$ | O O O O O O O |
$$ | X X X X X X X |
$$ | . . . . . X . |
$$ | . . . . . X . |
$$ -----------------[/go]

Can White prevent Black from making infinite passes?

Click Here To Show Diagram Code

[go]$$W
$$ -----------------
$$ | X X X X X X X |
$$ | . X 3 X 1 X O |
$$ | O O X O X O 2 |
$$ | O O O O O O O |
$$ | X X X X X X X |
$$ | . . . . . X . |
$$ | . . . . . X . |
$$ -----------------[/go]

Click Here To Show Diagram Code

[go]$$W pass
$$ -----------------
$$ | X X X X X X X |
$$ | 5 X O X O X 7 |
$$ | O O 8 O 6 O X |
$$ | O O O O O O O |
$$ | X X X X X X X |
$$ | . . . . . X . |
$$ | . . . . . X . |
$$ -----------------[/go]

Click Here To Show Diagram Code

[go]$$Wm9
$$ -----------------
$$ | X X X X X X X |
$$ | O X 3 X 1 X O |
$$ | O O X O X O 2 |
$$ | O O O O O O O |
$$ | X X X X X X X |
$$ | . . . . . X . |
$$ | . . . . . X . |
$$ -----------------[/go]

Etc. ad infinitum.
All moves from on are atari.

#############################
#############################

Can Black prevent White from making infinite passes?

Click Here To Show Diagram Code

[go]$$B
$$ -----------------
$$ | X X X X X X X |
$$ | 1 X 4 X 2 X O |
$$ | O O X O X O 3 |
$$ | O O O O O O O |
$$ | X X X X X X X |
$$ | . . . . . X . |
$$ | . . . . . X . |
$$ -----------------[/go]

Click Here To Show Diagram Code

[go]$$B
$$ -----------------
$$ | X X X X X X X |
$$ | X X O X O X 6 |
$$ | O O 7 O 5 O X |
$$ | O O O O O O O |
$$ | X X X X X X X |
$$ | . . . . . X . |
$$ | . . . . . X . |
$$ -----------------[/go]

Etc. ad infinitum.
All moves from on are atari.

_________________
The really most difficult Go problem ever: https://igohatsuyoron120.de/index.htm
Igo Hatsuyōron #120 (really solved by KataGo)

That means that you agree with me?
Can white prevents black to make infinite passes? NO
Can black prevents white to make infinite passes? YES
=> black has an advantageous loop

If you had a concrete example with 4 ko available, we could discuss this issue deeper ...

_________________
The really most difficult Go problem ever: https://igohatsuyoron120.de/index.htm
Igo Hatsuyōron #120 (really solved by KataGo)

Oh, sorry.

I thought the conclusion would be clear, given the pass stones below the diagrams.

_________________
The really most difficult Go problem ever: https://igohatsuyoron120.de/index.htm
Igo Hatsuyōron #120 (really solved by KataGo)

Yes OC here is an example:

Click Here To Show Diagram Code

[go]$$W
$$ ---------------------
$$ | . . . . . . . . . |
$$ | . . . . . . . . . |
$$ | . . . . X X X . . |
$$ | . X X X O O X X . |
$$ | X X O O X O O X X |
$$ | O O O X X X O O O |
$$ | O O X . X . X O O |
$$ | O O O X X X O O O |
$$ | . O . O X O . O . |
$$ ---------------------[/go]

Oops it does not seem to be the best example, I will try to find another. At least you can just try to identify what you mean by length of a cycle.

Click Here To Show Diagram Code

[go]$$W
$$ -----------------
$$ | . X X X X X X |
$$ | X X . X O X X |
$$ | O O X O . O O |
$$ | . O O O O O O |
$$ | O X X X X X X |
$$ | X X . . . X . |
$$ | . . . . . X . |
$$ -----------------[/go]

"Can White prevent Black from making infinite passes?"

What are infinite passes? After two successive passes, hypothetical play ends.

Black always passes and does not care whether his stones are removed therefore White cannot prevent Black from passing.

Apparently, you mean something else. Something like my "answer-force". Some dual strategy like "force local-2 permanent removal or an infinite cycle". Just guessing what you might mean.

Write down what you mean!

Next, you ask

"Can Black prevent White from making infinite passes?"

I suppose by posing two questions you try to invent status definitions similar to my basic ko type definitions with their typically four questions: http://home.snafu.de/jasiek/ko_types.pdf

English spelling: Japanese.

Look at https://lifein19x19.com/viewtopic.php?p=266766#p266766 where I have analysed this position for the first time.
At the very beginning of this post I clarified the objective of the corresponding hypothetical play (I am not sure it is good idea to introduce the wording "hypothetical play" in my rule but at least I understand what it means here in your post):
Is all the board black territory?
IOW, because there are no problem with the borders, the question becomes "is black able to build a two eye formation covering all the board?"
Keeping this in mind you know if you can afford to pass: if by passing you cannot not reach your ojective then you simply cannot pass.

Remember how works the confirmation phase. It is a loop with three points
1) A player claim that a set of location is her territory
2) Borders are verified
3) if borders are OK then the only purpose of the analyse is to know whether or not the player is able to build a two eye formation covering all the set of locations.

When you say "after two successive passes, hypothetical play ends" it is OC a wording remark for my proposal text. I am sure you have understood my idea : because we have to care about ko ban, obviously I have to add that the "hypothetical play" ends after three passes (remember I have no ko-pass nor pass-for-ko in my rule)