Things are becoming clearer now!



Ok, this is for S2.

(For a sequence, I speak of "net profit" instead of "gain", which is for a single move.)

Let me try to calculate for S1:

Black's previous net profit = T/2 - t/2,

White lets P be -23 1/3,

Black continues elsewhere for the net profit = t/2.

Altogether

(T/2 - t/2) + (-23 1/3) + t/2 = -23 1/3 + T/2.

However, this is not what you calculated when you got -23 1/3 + t. Apparently, there is more of your method I do not understand!

Again you are wrong Robert.
For S1, the previous net profit for black is not T/2 - t/2 but T/2 + t/2. This due to the fact that black played one more move in the environment than white.
S1 = -23 1/3 + (T/2 + t/2) + t/2 = -23 1/3 + T/2 + t

To summary the rule is simple:
if black is gote you add to the term -t
if white is gote you add to the term +t
in sente situation you do not add any term.

Starting in the rich environment at T results in the net profit T/2.

Starting in the rich environment at t results in the net profit t/2 for its continuing player.

Before White starts local play, alternating play in the rich environment started and stopped by Black, I see.

Therefore, White would be the continuing player in the rich environment if White chose it. From Black's perspective, the net profit of the continued rest of the rich environment would be -t/2.

Hence, the previous net profit of the rich environment is -t/2 smaller than the net profit T/2 of the whole rich environment, that is,

T/2 - (-t/2) = T/2 + t/2.

As you have advertised. Phew! How many mistakes have I made this time?

Good Robert, now you can try to understand my "always good exchange strategy".

Let me show you a second example:

Click Here To Show Diagram Code

[go]$$W diag 1
$$ ----------------------------
$$ . . . . . . . b c . . . . |
$$ . . . . . . . . . a O . . |
$$ . . . . . . . X O . X O . |
$$ . . X , . X . X X X . O . |
$$ . . . . . . . . . . O . . |
$$ . . . . . . . . . . O . . |
$$ . . . . . . . . . . . . . |
$$ . . . . . . . . . . . . . |
$$ . . . . . . . . . . O . . |
$$ . . . , . . . . . , . . . |[/go]

Let's put position P in a rich environment with a high temperature T and consider the game G made of position P, this environment, and black to play.
Assume white b is sente. That means that the score of the game G (here again I do not write the T/2 term though I do not ignore it!) is, with this sente white move "b", S1 = +2.

The question is now the following : is white able to reach a better score than +2 (a score less than +2) by using white option "a"?

Now I begin the "Always good exchange strategy".

Click Here To Show Diagram Code

[go]$$W diag 2
$$ ----------------------------
$$ . . . . . . . . 2 . . . . |
$$ . . . . . . . . . 1 O . . |
$$ . . . . . . . X O . X O . |
$$ . . X , . X . X X X . O . |
$$ . . . . . . . . . . O . . |
$$ . . . . . . . . . . O . . |
$$ . . . . . . . . . . . . . |
$$ . . . . . . . . . . . . . |
$$ . . . . . . . . . . O . . |
$$ . . . , . . . . . , . . . |[/go]

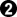
First of all after white I decide to answer (without knowing if it the best move!)

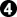
From this diag 2 I claim that the following exchange is a good exchange for white (whitout saying that this moves are the best ones).

Click Here To Show Diagram Code

[go]$$W diag 3
$$ ----------------------------
$$ . . . . . . . . 2 . . . . |
$$ . . . . . . . 4 3 1 O . . |
$$ . . . . . . . X O . X O . |
$$ . . X , . X . X X X . O . |
$$ . . . . . . . . . . O . . |
$$ . . . . . . . . . . O . . |
$$ . . . . . . . . . . . . . |
$$ . . . . . . . . . . . . . |
$$ . . . . . . . . . . O . . |
$$ . . . , . . . . . , . . . |[/go]

That means that the score white can reach from diag 3 is for white an upper bound of the score white can reached from diag 2.

From this diag 3 I claim now that the following exchange is still a good exchange for white (still whitout saying that this moves are the best ones).

Click Here To Show Diagram Code

[go]$$W diag 4
$$ ----------------------------
$$ . . . . . . . 6 2 5 . . . |
$$ . . . . . . . 4 3 1 O . . |
$$ . . . . . . . X O . X O . |
$$ . . X , . X . X X X . O . |
$$ . . . . . . . . . . O . . |
$$ . . . . . . . . . . O . . |
$$ . . . . . . . . . . . . . |
$$ . . . . . . . . . . . . . |
$$ . . . . . . . . . . O . . |
$$ . . . , . . . . . , . . . |[/go]

That means that the score white can reach from diag 4 is for white an upper bound of the score white can reached from diag 3 => the score white can reach from diag 4 is for white an upper bound of the score white can reached from diag 2

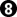
Finally from diag 4 the following exchange is still a good exchange for white

Click Here To Show Diagram Code

[go]$$W diag 4
$$ ----------------------------
$$ . . . . . . . 6 2 5 . . . |
$$ . . . . . . . 4 3 1 O 7 . |
$$ . . . . . . . X O 8 X O . |
$$ . . X , . X . X X X . O . |
$$ . . . . . . . . . . O . . |
$$ . . . . . . . . . . O . . |
$$ . . . . . . . . . . . . . |
$$ . . . . . . . . . . . . . |
$$ . . . . . . . . . . O . . |
$$ . . . , . . . . . , . . . |[/go]

Do you see what means "always good exchange strategy"?

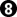
Using this sequence the score of the game is +2. That means that with option white "a" white cannot reach a score less than +2 => white "a" cannot be better than white "b".

I try to understand always good exchange strategy.

You consider a local sente sequence comprising pairs of moves called exchanges.

So much I understand. Everything below is my first guesswork of what you might mean.

You choose an arbitrary local move 2.

Suppose you have already made n exchanges creating an intermediate position P_n.

S_n is the [perfect play] score of P_n.

Consider an arbitrary exchange n+1.

Pretend (this is what I understand: that you pretend it) that S_n+1 compares to S_n, this I do not understand, how? At least? At most? From which player's perspective?

From all the arbitrary choices and pretences, imply something particular for move 1 as an alternative option for a known sente move 1.

As you see, I understand almost nothing of your explanation so far.

OK Robert let's go slowly

Click Here To Show Diagram Code

[go]$$B
$$ ---------------------------
$$ | O . X X . . b . X . X . .
$$ | O O . O X . O a O X X . .
$$ | . O O O . O O X O X . . .
$$ | . . . O O O . X O X . . .
$$ | . . . . . O X X O X . . .
$$ | . . . . . O O O O X . . .
$$ | . . . . . . . . . . . . .[/go]

Let's build position G made of this position P, a rich environment at a high temperature T and black to play.
Considering only black option "a" then the best score for this game G is S1 = -17.66.

Click Here To Show Diagram Code

[go]$$B
$$ ---------------------------
$$ | O . X X . . 1 . X . X . .
$$ | O O . O X . O . O X X . .
$$ | . O O O . O O X O X . . .
$$ | . . . O O O . X O X . . .
$$ | . . . . . O X X O X . . .
$$ | . . . . . O O O O X . . .
$$ | . . . . . . . . . . . . .[/go]

Now let's consider the option 1. The question is the following : with this option can black reach a score S2 so that S2 > S1?
If after the best score is S2, then whatever the white answer, white cannot reached a score less than S2.

Click Here To Show Diagram Code

[go]$$B
$$ ---------------------------
$$ | O . X X . . 1 . X . X . .
$$ | O O . O X . O 2 O X X . .
$$ | . O O O . O O X O X . . .
$$ | . . . O O O . X O X . . .
$$ | . . . . . O X X O X . . .
$$ | . . . . . O O O O X . . .
$$ | . . . . . . . . . . . . .[/go]

Assume I decide to play the above. Let's call S3 the best score after
Because I do not know if is the best white answer (a white move in the environment might be better) that means that the may be a mistake => S3 >= S2

Click Here To Show Diagram Code

[go]$$B
$$ ---------------------------
$$ | O . X X . 4 1 3 X 5 X . .
$$ | O O . O X 6 O 2 O X X . .
$$ | . O O O . O O X O X . . .
$$ | . . . O O O . X O X . . .
$$ | . . . . . O X X O X . . .
$$ | . . . . . O O O O X . . .
$$ | . . . . . . . . . . . . .[/go]

Now comes the exchange
Here is the point: the black GO PLAYER (and not the theory!) tell us black will be happy if the exchange takes places. That is a very valuable new information and if the theory can take into account this new information then the efficiency of the theory can greatly increase.
Now you continue with the theory. Let's call S4 the best score after
Because the exchanges are good for black that means that S4 >= S3
At this point we have S4 >= S3 >= S2 => S4 >= S2
If now you find S4 = -19 that means that S4 = -19 >= S2
Now remenber the black option "a" : S1 = -17.66
You conclude that
S1 = -17.66 > -19 >= S2 => S1 > S2 => option "a" is better than option "b".

Taking you last post you see that I do not consider "an arbitrary exchange" but rather a "good exchange" for black.

In CGT style contexts, "score" is a perfect play / best / correct score, so there is no need to call it "best score".

If something is a mistake, we do not have equality. So do not write "S3 >= S2" but write "S3 > S2". However, you speak about "may be a mistake" meaning "is correct or a mistake". Therefore, S3 >= S2 is ok.



Let me rephrase this:

Click Here To Show Diagram Code

[go]$$B
$$ ---------------------------
$$ | O . X X . . 1 . X . X . .
$$ | O O . O X . O . O X X . .
$$ | . O O O . O O X O X . . .
$$ | . . . O O O . X O X . . .
$$ | . . . . . O X X O X . . .
$$ | . . . . . O O O O X . . .
$$ | . . . . . . . . . . . . .[/go]

Now let's consider the option 1 of Black 1 and its score S2. We ask: Is S2 > S1?

Click Here To Show Diagram Code

[go]$$B
$$ ---------------------------
$$ | O . X X . . 1 . X . X . .
$$ | O O . O X . O 2 O X X . .
$$ | . O O O . O O X O X . . .
$$ | . . . O O O . X O X . . .
$$ | . . . . . O X X O X . . .
$$ | . . . . . O O O O X . . .
$$ | . . . . . . . . . . . . .[/go]

Assume White chooses :w2: resulting in the score S3.

Since we do not know if :w2: is correct or a mistake (e.g., a white move in the environment might be better), S3 >= S2.

(I will try to understand the rest later.)

Good understanding Robert, for this first part.

No. You say too much. We do not know whether the exchanges are good for black. We only know that Black says so! You may say: "Assuming S4 >= S3, [...]"

Now, what is the "always good exchange strategy"? What is its description for a particular, arbitrary starting player?

No Robert your are wrong. When I say "the black GO PLAYER is happy if the exchange takes places" I do not ASSUME it is the case, I am really sure these exchanges cannot be bad for black!

Click Here To Show Diagram Code

[go]$$B
$$ ---------------------------
$$ | O . X X . . X a X . X . .
$$ | O O . O X . O O O X X . .
$$ | . O O O . O O X O X . . .
$$ | . . . O O O . X O X . . .
$$ | . . . . . O X X O X . . .
$$ | . . . . . O O O O X . . .
$$ | . . . . . . . . . . . . .[/go]

In the position above let's assume it is black to play. Robert, do you see that the ONLY correct LOCAL black move is the move at "a"? If not I really cannot help you.
Let's continue with only the following assumption : you are convinced that, in the diagram above, the ONLY correct local black move is the move at "a".
Let's add a rich environment and call S3 the resulting score. Now imagine the following scenario of the correcponding game : black chooses always the best moves while I force white to follow black moves (if the last black move is in the environment then white must play in the environment and if the last black move is a local play then white must answer locally). Because all black moves are the best ones the resulting score S4 of this scenario cannot be bad for black (S4 >= S3).
The point is that the above scenario is very easy to visualize:
Black plays in the environment (=> white must also play in he environment in accordance to the scenario) till the temperature drops to a certain temperature t1 at which it is better for black to play locally (instead of playing in the environment).

Click Here To Show Diagram Code

[go]$$B
$$ ---------------------------
$$ | O . X X . 4 X 3 X . X . .
$$ | O O . O X . O O O X X . .
$$ | . O O O . O O X O X . . .
$$ | . . . O O O . X O X . . .
$$ | . . . . . O X X O X . . .
$$ | . . . . . O O O O X . . .
$$ | . . . . . . . . . . . . .[/go]

At temperature t1 black plays at (the best move for black) and I force white to answer at (this white answer may not be the best move for white).

Click Here To Show Diagram Code

[go]$$B
$$ ---------------------------
$$ | O . X X . O X X X 5 X . .
$$ | O O . O X 6 O O O X X . .
$$ | . O O O . O O X O X . . .
$$ | . . . O O O . X O X . . .
$$ | . . . . . O X X O X . . .
$$ | . . . . . O O O O X . . .
$$ | . . . . . . . . . . . . .[/go]

Continuing the game with the same scenario black will then be able to play the best move and I forced white to answer (and here again this white answer may not be the best move for white).

The final result of this game under this scenario is S4 (here S4 = -19).
Because we know that S3 <= S4 then we have to conclude S3 <= -19.
Do you understand Robert?

Not always when you say I was wrong I am. "The black go player is happy", "you are sure" and any possible proofs for clearer assumptions are different things.

If you try to prove something or convince me of your conviction informally, I am not convinced.

In general, I am not convinced about Black 'a' yet because the single stone connection might be better as a negative ko threat. If the environment is only the remaining rich one, some proof might be easier but until then I am not convinced there, either. I have seen too many values anomalies in allegedly simplistic environments.

I understand your basic S1 <= S2 <=.. scheme but your overall argument is too informal to convince me. I suspect I might write down your always good exchange strategy carefully but I do not do your work. You are the one who wants to convince us that it is meaningful and useful.

JFTR, I do not oppose semi-formal strategic theory for go players, but I do not buy it as a formal theory without sufficient formal explanation.

If you introduce local ko threat arguments that means that you introduce also a possible ko in the environment but in that case you cannot expect to be able to compare two local options. Even two apparently simple gote areas cannot be compared if a ko can take place in the environment.

Robert, do not try to write my always good exchange strategy.

Click Here To Show Diagram Code

[go]$$B
$$ ---------------------------
$$ | O . X X . . b . X . X . .
$$ | O O . O X . O a O X X . .
$$ | . O O O . O O X O X . . .
$$ | . . . O O O . X O X . . .
$$ | . . . . . O X X O X . . .
$$ | . . . . . O O O O X . . .
$$ | . . . . . . . . . . . . .[/go]

When I apply this theory to the position above, with the two options "a " and "b", I use only a basic case of the "always good exchange strategy". If you have some doubt on the way I proofed black option "b" cannot be better than option "a" then I am 100% sure that you cannot be convinced by the general "always good exchange strategy".
Forget this strategy and try to understand my proof on the example above.

What is not acceptable as a proof in my reasonning?
Let's build a game G made of position P, a rich environment at high temperature and black to play.
In this game, assume that black is able to play the option black "b", and call S2 the score of the resulting position P' reached after black "b".
From that position P' assume the game continue with the best black moves but not necessarily the best white moves. if you call S4 the score of this last game do you have doubt concerning the claim : S4 >= S2 ?

Any necessary definitions may come first.

Separate conjecture and proof.

State a conjecture before a proof (attempt).

Avoid informal text in definitions, conjectures and proofs, such as "is able to" or "do you have doubt".

Any assumptions in a conjecture can be presuppositions.

Any assumptions in a proof serve different purposes.

What do you mean Robert? I did not show you a formal method and, as consequence, we are surely not discussing my method itself.
I only handled an example (by using the basis of my method) : I build a position G made of position P, a rich environment at high temperature and black to play, and starting from this position G, I compared the result of the game G when black decides to use option "a" and when black decides to use instead option b.
On this specific example and in this specific context my goal was only to proof that black option "a" was better than black option "b" (better meaning simply a better result for the game G).
Can you clarify where are your doubts concerning my proof attempt on THIS example?

The same. What you are trying to show for this one example can be done by informal guesswork, which so far does not convince me at all, or by formal maths, which might convince me if done well.

As long as you do not state your method clearly and, in application, mix informal / formal and conjecture / "proof", chances are low that I understand and become convinced.

Besides, stop pretending it would be just an example while you use general parameters and relations.

No Robert I can only propose to apply my method on some examples for a very simple reason : though my method is quite clear in my head I never wrote it formely on paper and, as you know perfectly, this work would be a hard job I do not wish to do.
In this context, if you are not interested in the way I compare various options you can just ignore it OC and let other readers understand how I proceed.

Click Here To Show Diagram Code

[go]$$B
$$ ---------------------------
$$ | O . X X . . b . X . X . .
$$ | O O . O X . O a O X X . .
$$ | . O O O . O O X O X . . .
$$ | . . . O O O . X O X . . .
$$ | . . . . . O X X O X . . .
$$ | . . . . . O O O O X . . .
$$ | . . . . . . . . . . . . .[/go]

BTW, using your own method, can you show us how do you compare black options "a" and "b"? With what result?

See earlier in this thread.

I am not quite sure but you seem to say that the position is gote => option "a" is better than option "b".
I do not know your method, you do not know mine but ... same result !

A name of a local endgame indicates what is usually - not always - correct.