Thanks John Fairbairn !
Diagram 2 (p.4)
* 黒二で若し三、と受ければ白も十七と應ずる位のものであつたらう乎。
若し moshi if/in case/supposing
受ければ ukereba conditional of ukeru
應ずる ouzuru answer, reply, accept
位 kurai
もの mono thing
乎 ka question mark
This is a hard one, with two main problems:
- what to do with kurai no mono? Literally, it seems to mean "a thing of the sort", "something like" but I found references online to an idiom kurai no mono having something to do with "only, the only thing"
- -rau ka, Based on Henderson's (
Handbook of Japanese Grammar) example
mono no nijuudo mo yattarō ka "I probably tried it twenty times, I guess", I take it as indicating probability. But comments in the same book make me wonder wether this should be understood as expressing doubt.
So at this stage I have several possible translations (none of which even close to the solution I guess

). The first two differ by the nuance given by
kurai no mono and the last one takes -rau ka as expressing doubt rather than probability.
Translation(s)"At black 2, if (black) defends with 3, there was probably a thing of the sort of white also answering with 17, I guess." >
"
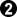
, if black defends at 3, white would also probably have answered with something like 17."
"
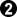
, if black defends at 3, white also could probably only have answered with 17."
"
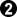
, if black defends at 3, I doubt white would also have answered with something like 17."
(17 being the marked intersection)
- Click Here To Show Diagram Code
[go]$$Wcm1
$$ ---------------------------------------
$$ | . . . . . . . . . . . . . . . . . . . |
$$ | . . . . . . . O O . . . . . . 1 . . . |
$$ | . . . . O O . X X O O . . M . . 3 . . |
$$ | . . X , . X . X . X . . . . . X . . . |
$$ | . . . X . . . . X . . . . . . . . . . |
$$ | . . . . . . . . . . . . . . . X . . . |
$$ | . . . . . . . . . . . . X . . X . . . |
$$ | . . . . . . . O . . O . . . O X . . . |
$$ | . . O O X . X O . . . . X . . O X . . |
$$ | . . . X X . . X O O . O X . . O X . . |
$$ | . O . . . . X . . . . . X . . O . . . |
$$ | . . . . . . . X . O . X . . . O X . . |
$$ | . . . . . . . . . X O . X O O . X . . |
$$ | . O O . O . . . X O O . X X O . X . . |
$$ | . . X . . . X X X X O . X O O O . . . |
$$ | . . . X . X X O X X O . X O X , O . . |
$$ | . . O . O . X O O O O . X O X O . . . |
$$ | . . . O X O X . . . . . 2 . . . . . . |
$$ | . . . . . . . . . . . . . . . . . . . |
$$ ---------------------------------------[/go]



